The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of an edge is 10 centimeters?

Let V be volume of cube of side x
$therefore space space space space space space space space space straight V space equals space straight x cubed From space given space conditions comma space space space space space space space space space space space space space space space space space space space space space space dV over dt space equals space 9 space cm cubed divided by straight s therefore space space space space space space straight d over dt left parenthesis straight x cubed right parenthesis space equals space 9 space space space space space space space space space space space space space space rightwards double arrow space space space space 3 straight x squared dx over dt space equals 9 space space space space space space space space space space space space space space space rightwards double arrow space space space dx over dt space space equals space 3 over straight x squared space space space space space space space space space space space... left parenthesis 1 right parenthesis$
Let S be surface area of cube
$therefore space space space space space space space straight S space equals space 6 straight x squared$
Rate of increasing of surface area = $dS over dt space equals space straight d over dt left parenthesis 6 straight x squared right parenthesis$

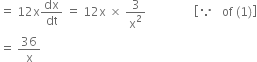
$equals space 12 straight x dx over dt space equals space 12 straight x space cross times space 3 over straight x squared space space space space space space space space space space space space space space space space open square brackets because space space space of space left parenthesis 1 right parenthesis close square brackets equals space 36 over straight x$
When x = 10, rate of increase of surface area = $36 over 10 space equals space 3.6 space cm squared divided by straight s$

102 Views

Application of Derivatives

Hope you found this question and answer to be good. Find many more questions on Application of Derivatives with answers for your assignments and practice.

Mathematics Part I

Browse through more topics from Mathematics Part I for questions and snapshot.