In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i)    ∆APD ≅ ∆CQB
(ii)   AP = CQ
(iii)  ∆AQB ≅ ∆CPD
(iv)  AQ = CP
(v)   APCQ is a parallelogram.

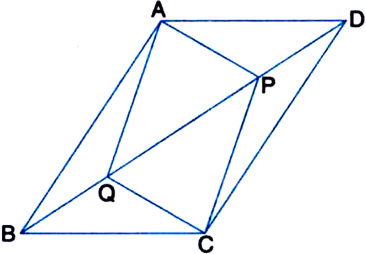
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ.
To Prove: (i) ∆APD ≅ ∆CQB
(ii)     AP = CQ
(iii)    ∆AQB ≅ ∆CPD
(iv)    AQ = CP
(v)     APCQ is a parallelogram.
Construction: Join AC to intersect BD at O.
Proof: (i) In ∆APD and ∆CQB,
∵ AD || BC
| Opposite sides of parallelogram ABCD and a transversal BD intersects them
∴ ∠ADB = ∠CBD
| Alternate interior angles
⇒ ∠ADP = ∠CBQ    ...(1)
DP = BQ    | Given (2)
AD = CB    ...(3)
| Opposite sides of ||gm ABCD In view of (1), (2) and (3)
∆APD ≅ ∆CQB
| SAS congruence criterion
(ii)    ∵ ∆APD ≅ ∆CQB
| Proved in (i) above
∴ AP = CQ    | C.P.C.T.
(iii)    In ∆AQB and ∆CPD,
∵ AB || CD
| Opposite sides of ||gm ABCD and a transversal BD intersects them
∴ ∠ABD = ∠CDB
| Alternate interior angles
⇒ ∠ABQ = ∠CDP
QB = PD    | Given
AB = CD
| Opp. sides of || gm ABCD
∴ ∆AQB ≅ ∆CPD | SAS Congruence Rule
(iv) ∵    ∆AQB = ∆CPD
| Proved in (iii) above
∴ AQ = CP    | C.P.C.T.
(v)    ∵ The diagonals of a parallelogram bisect each other.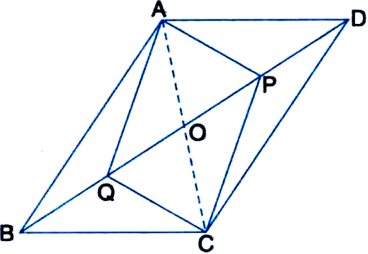


∴ OB = OD
∴ OB - BQ = OD - DP
| ∵ BQ = DP (given)
∴ OQ = OP    ...(1)
Also, OA = OC    ...(2)
| ∵ Diagonals of a || gm bisect each other
In view of (1) and (2), APCQ is a parallelogram.