(a) State the principle of the working of a moving coil galvanometer, giving its labelled diagram.
(b) “Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity.” Justify this statement.
(c) Outline the necessary steps to convert a galvanometer of resistance RG into an ammeter of a given range.
a) Principle of moving galvanometer:
A current carrying coil when kept inside a uniform magnetic field, can experience a torque.
When current (I) is passed in the coil, torque acts on the coil given by, 
where q is the angle between the normal to plane of coil and the magnetic field of strength B,
N is the number of turns in a coil.
When the magnetic field is radial, as in the case of cylindrical pole pieces and soft iron core, then in every position of coil the plane of the coil, is parallel to the magnetic field lines, so that
 = 90° and sin 90° =1
= 90° and sin 90° =1
Deflecting Torque is given by, 
If C is the torsional rigidity of the wire and q is the twist of suspension strip, then restoring torque =C
For equilibrium, deflecting torque = restoring torque,
That is, deflection of coil is directly proportional to current flowing in the coil.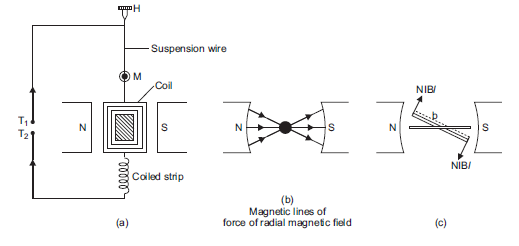
b) 
Clearly, the voltage sensitivity is dependent on current sensitivity and the resistance of the galvanometer. If we increase current sensitivity and resistance G is larger, then it is not certain that voltage sensitivity will be increased. Thus, the increase of current sensitivity does not imply the increase of voltage sensitivity.
c)
Conversion of galvanometer into ammeter:
In order to convert galvanometer into ammeter a shunt resistance i.e., a small resistance in parallel is connected across the coil of galvanometer.
Let G be the resistance of galvanometer and Ig the current required for full scale deflection.
Suppose this galvanometer is to converted into ammeter of range I ampere and the value of shunt required is S.
If, Is is the current in the shunt, then 
which is the required expression for conversion of galvanometer into ammeter.
