The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is:

• 0.5π

• π

• 0.707 π

• 0.707 π

A.

0.5π

The displacement equation of particle executing SHM is

x = a cos ( ωt +Φ)  .. (i)

velocity, v = dx/dt = - aω sin (ωt + Φ)  .. (ii)

and acceleration,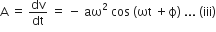




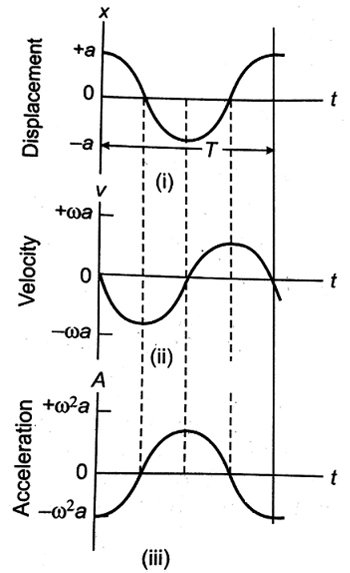
Fig (i) is a plot of eq (i) with Φ = 0. Fig (ii) shows Eq. (ii) also with Φ = 0 fig (iii) is a plot of Eq (iii) . it should be noted that in the figures the curve of v is shifted (to the left) from the curve of x by one - equate period (T/4).Similarly, the acceleration curve of A is shifted (to the left) by T/4 relative to the velocity curve of v. This implies that velocity is 90^o C (0.5 π) out phase with the displacement and the acceleration is 90^o C (0.5 π) out of phase with the velocity but 180^o  π out phase with displacement.