Uses of concave mirrors:
1. Shaving mirror: A concave mirror is used as a shaving or make-up mirror because it forms erect and enlarged image of the face when it is held closer to the face.
2. As head mirror: E.N.T. specialists use a concave mirror on their forehead. The light from a lamp after reflection from the mirror is focussed into the throat, ear or nose of the patient making the affected part more visible.
3. In ophthalmoscope: It consists of a concave mirror with a small hole at its centre. The doctor looks through the hole from behind the mirror while a beam of light from a lamp reflected from it is directed into the pupil of patient’s eye which makes the retina visible.
4. In headlights: Concave mirrors are used as reflectors in headlights of motor vehicles, railway engines, torch lights, etc. The source is placed at the focus of the concave mirror. The light rays after reflection travel over a large distance as a parallel beam of high intensity.
5. In astronomical telescopes: A concave mirror of large diameter (5 m or more) is used as objective in an astronomical telescope. It collects light from the sky and makes visible even those faint stars which cannot be seen with naked eye.
6. In solar furnaces: Large concave mirrors are used to concentrate sunlight to produce heat in solar furnace.

Uses of convex mirrors: Drivers use convex mirror as a rear-view mirror in automobiles because of the following two reasons:
1. A convex mirror always forms an erect, virtual and diminished image of an object placed anywhere in front of it.
2. A convex mirror has a wider field of view than a plane mirror of the same size, as shown in the fig.
Thus convex mirrors enable the driver to view much larger traffic behind him than would be possible with a plane mirror. The main disadvantage of a convex mirror is that it does not give the correct distance and the speed of the vehicle approaching from behind.

Fig.  Field of view of (a) a plane mirror (b) a convex mirror

New cartesian sign convention for reflection by spherical mirrors: According to this convention:
1. The object is on the left of the mirror. So all the ray diagrams are drawn with the incident light travelling from left to right.
2. All the distances parallel to the principal axis are measured from the pole of the mirror.
3. All distances measured in the direction of incident light are taken as positive.
4. All distances measured in the oppsoite direction of incident light are taken as negative.
5. Heights measured upwards and perpendicular to the principal axis are taken positive.
6. Heights measured downwards and perpendicular to the principal axis are taken negative.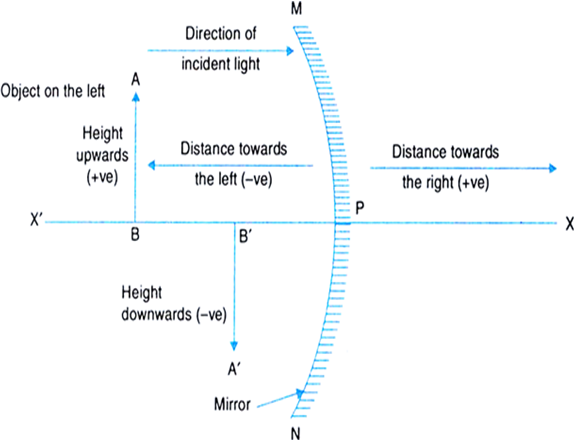

Fig. New cartesian sign convention for reflection of light by spherical mirrors

New cartesian sign convention:

The pole P of the spherical mirror is taken as the origin and the principal axis of the mirror is along the X-axis of the coordinate system. 

Keeping this in mind, we can easily note the following facts: 

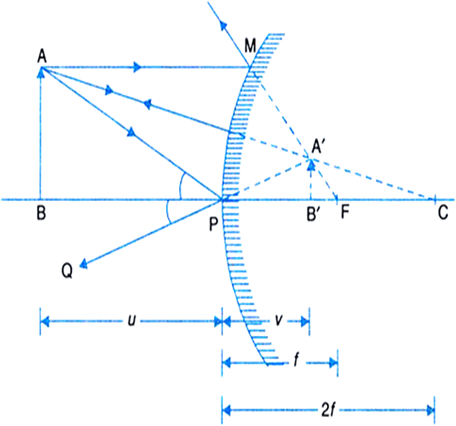
(i) Object distance, u is always taken negative, because the object is placed on the left of the mirror. 

(ii) In case of a concave mirror, a real image is formed in front (left side) of the mirror and a virtual image is formed behind (right side) the mirror, so image distance v is negative for a real image and positive for a virtual image. 

(iii) In case of a convex mirror, the image distance v is always positive because the image is formed behind the mirror and is virtua. 

(iv) The object height h is always taken positive, because the object is placed above the principal axis. 

(v) The image height h' is taken negative for real image (as it lies below the principal axis) and the image height h' is taken positive for a virtual image (as it lies above the principal axis). 

(vi) The focal length and radius of curvature of a concave mirror are taken negative because the principal focus lies on the left of the mirror. 

(vii) The focal length and radius of curvature of a convex mirror are taken positive, because the principal focus lies on the right hand side of the mirror.