We have :
x - y = 1
⇒    x = y + 1
Thus, we have following table :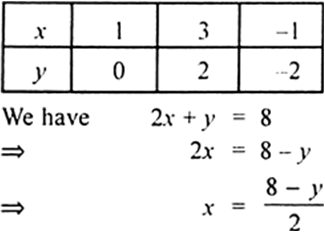

Thus, we have following table :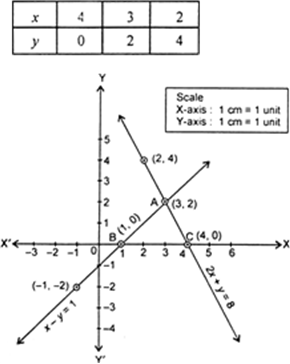

Fig. 3.21.

When we plot the graph of the given equations, we find that both the lines intersect at the point (3, 2), therefore x = 3, y = 2 is the solution of the given system of equations.

Vertices of triangle are A(3, 2), 13(1, 0), C(4, 0).

We have x = y
Thus, we have following table :

We have,    y = 2x
Thus, we have following table :

We have x + y = 6
⇒    x = 6 - y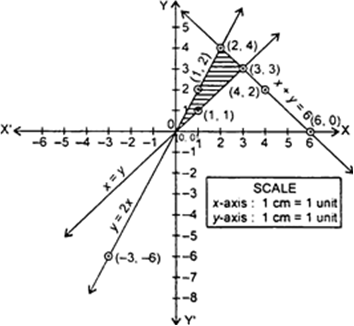

Fig. 3.20.

Thus, we have following table :

Co-ordinates of the vertices are (0, 0), (2, 4), (3, 3).

We have,
3x + y - 5 = 0
⇒ y = 5 - 3x
Thus we have following table :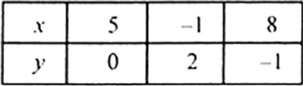

We have, 2x - y - 5 = 0
⇒    y = 2x - 5
Thus, we have following table :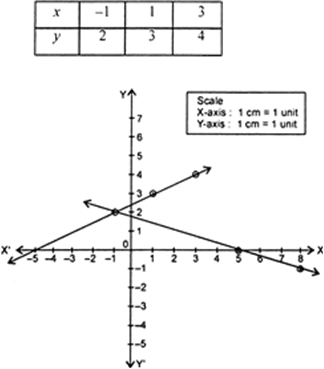

Fig. 3.19.

When we plot the graph of the given equation, we find that both the lines intersect at the point (-1, 2), therefore x = -1, y = 2 is the solution of the given system of equations.
From the graph we observe that lines intersect y-axis at (-5, 0) and (5,0)

Let the cost of 1 bat be Rs. x and cost of I ball be Rs.y
Case I. Cost of 3 bats = 3x
Cost of 6 balls = 6y
According to question,
3x + 6y = 3900
Case II. Cost of I bat = x
Cost of 3 more balls = 3y
According to question,
x + 3y = 1300
So, algebraically representation be
3x + 6y = 3900
x + 3y = 1300
Graphical representation :
We have,    3x + 6y = 3900
⇒    3(x + 2y) = 3900
⇒    x + 2y = 1300
⇒    a = 1300 - 2y
Thus, we have following table :

We have,    x + 3y = 1300
⇒    x = 1300 - 3y
Thus, we have following table :

When we plot the graph of equations, we find that both the lines intersect at the point (1300. 0). Therefore, a = 1300, y = 0 is the solution of the given system of equations.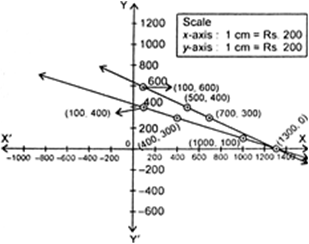

We have
x + y = 5
⇒    x = 5 - y
Thus, we have the following table :

We have 3x - y = 3
⇒    y = 3x - 3
Thus, we have following table :

Fig. 3.22.

When we plot the graph of the given equations, we find that both the lines intersect at the point (2, 3), therefore, x = 3, y = 2 is the solution of the given system of equation.