Calculate Karl Pearson’s correlation co-efficient bv the assumed mean method.

X	14	15	18	20	25	30
Y	40	45	65	28	30	40

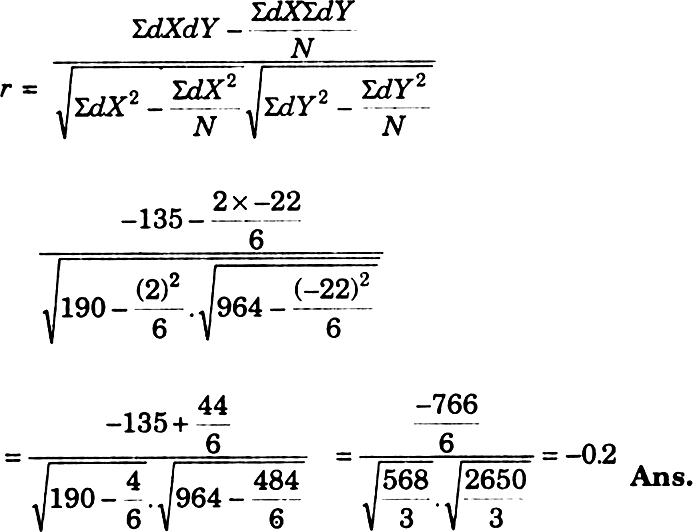
Calculate of Karl Pearson’s correlation co-efficient.

A.M. of X series =20 A.M. of Y series = 45

Perfect correlation is that where changes in two related variables are exactly proportional. It is of two types:

(i) Positive perfect correlation and (ii) Negative perfect correlation.

There is perfect positive correlation between the two variables of equal proportional changes are in the same direction. It is expressed as +1. If equal proportional changes are in the reverse direction. Then there is negative perfect correlation and it is described as –1.

(a) Example of positive perfect correlation

Price (Rs): 1 2 3 4 5

Supply (units) : 10 20 30 40 50

(b) Example of perfect negative correlaion

Price (Rs): 1 2 3 4 5

Demand (units) : 50 40 30 20 10 Q. 5. Define simple, and partly correlation.

Ans. Simple Correlation : When the relationship between two variables is studied and of these two variables one is independent and the other is dependent, then such correlation is called simple correlation. For example, relationship between income and expenditure.

Partial Correlation : When more than two variables are involved and out of these the relationship between two variables is studied only treating other variables as constant, then such correlation is partial.

Positive Correlation : When two variables move in the same direction, that is when one increases the other also increases and when one decreases the other also decreases then such a relation is called Positive correlation. For example, the relation between price and supply.

Increase in the value of both variables.

X : 10 20 30 40

Y : 100 150 200 250

2. Negative Correlation : When two variables change different directions, it is called negative correlation. For example relationship between price and demand. When prices rises other things remaining constant demand falls and when price falls demand rises.

X : 1 2 3 4

Y : 5 4 2 1

X : 10 20 30 40

Y : 100 150 200 250

The co-efficient of correlation of Karl Pearson’s is the quantitative measure of the relationship of two variables X and Y. It is represented by r. It is based on arithmetic mean and standard deviation. The co-efflciant of correlation (r) of two variables is obtained by dividing the sum of the products of the corresponding deviations of the various items of the two series from their respective means by the product of their standard deviation and the number of pairs of observations. Symbolically.

Limited degree of correlation coefficient: The value of correlation coefficient lies between minus one and plus one. The calculated result of correlation must valy between -1 to +1. Symbolically.

Rank collection co-efficient and simple correlation coefficient have the same interpretation. Its formula has been derived from simple correlation coefficient where individual values have been replaced by rank. These ranks are used for the calculation of correlation. This coefficient provides a measure of linear association between ranks assigned to units not their values correlation. Following formula is used for calculating rank correlation

In Karl Pearson’s coefficient of correlation, the values of two series are not assigned rank. The correlation coefficient provides a measure of linear association to the values of the variables. Following formula i.e. used for calculating the correlation coefficient.