The length of the common chord of the circles of radii 15 and 20, whose centres are 25 unit of distance apart, is
12
16
24
25
C.
24

The radius of the larger circle lying in the first quadrant and touching the line 4x + 3y - 12 =0 and the co-ordinate axes,is
5
6
7
8
B.
6
Let the equation of the circle is
x2 + y2 + 2gx +2fy +c =0
Thus circle touch the coordinate axes and lying in the first quadrant, then
g2 - c =0 and f2 - c = 0
The parabola with directrix x + 2y - 1 = 0 and focus (1, 0) is
4x2 - 4xy + y2 - 8x + 4y + 4 = 0
4x2 + 4xy + y2 - 8x + 4y + 4 = 0
4x2 + 5xy + y2 + 8x - 4y + 4 = 0
4x - 4xy + y - 8x - 4y + 4 = 0
A.
4x2 - 4xy + y2 - 8x + 4y + 4 = 0
Let P(x, y) be any point on the parabola
By defination of Parabola PM = PS
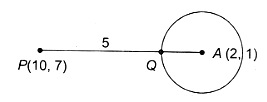
Consider the circle x2 + y - 4x - 2y + c = 0 whose centre is A(2, 1). If the point P(10, 7) is such that the line segment PA meets the circle in Q with PQ = 5, then c is equal to
- 15
20
30
- 20
D.
- 20
Let M be the foot of the perpendicular from a point P on the parabola y = 8(x - 3) onto its directrix and let S be the focus ofthe parabola. If SPM is an equilateral triangle, then P is equal to
C.

Let coordinate of P (h + at2, k + 2at) = P(3 + 2t2, 4t)
Then, coordinate of M(- 5, 4t)
We know that the side of this equilateral trianle is 4a = 4 x 2 = 8
Now, PS = 8
