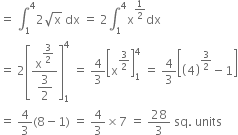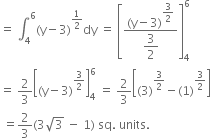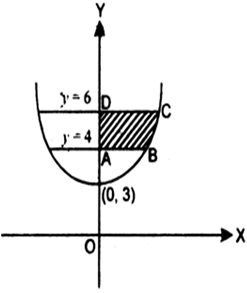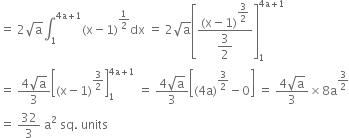
Find the area of the region bounded by x2 = 16 y, y = 1, y = 4 and the y-axis in the first quadrant.
The equation of curve is
![]()
Required area = ![]()
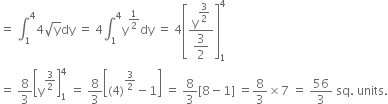
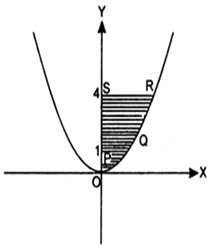
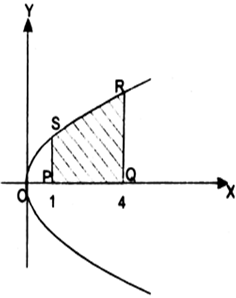
Find the area of the region bounded by y2 = 4 x, x = 1, x = 4 and the x-axis in the first quadrant.