A factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows:
| Machine | Area occupied | Labour force | daily output ( in units ) |
| A | 1000 m2 | 12 men men | 60 |
| B | 1200 m2 | 8 men | 40 |
He has maximum area of 9000 m2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output?
Let x and y respectively be the number of machines A and B, which the factory owner should buy.
Now according to the given information, the linear programming problem is:
maximise Z = 60x + 40y
Subject to the constraints
1000x + 1200 y 9000
The inequalities (1), (2), and (3) can be graphed as:

The shaded portion OABC is the feasible region.
The value of Z at the corner points are given in the following table.
| corner point | Z = 60x + 40y | |
| 0(0, 0) | 0 | |
| A | 300 | |
| B | 360 | maximum |
| C (6, 0) | 360 | Maximum |
The maximum value of Z is 360 units, which is attained at B, and c( 6, 0 ).
Now the number of machines cannot be in fraction.
Thus, to maximise the daily output, 6 machines of type A and no machine of type B need to be bought.
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand - operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operated machines to manufacture a packet of screws ‘B’. Each machine is available for at most 4 hours on any day. The manufacturer can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit.
Let the factory manufactures x screws of type A and y screws of type B on each day.
∴ x ≥ 0, y ≥ 0
Given that
| Screw A | Screw B | Availability | |
| Automatic Machine | 4 | 6 | 4 x 60 = 240 minutes |
| Hand operate machine | 6 | 3 | 4 x 60 = 240 minutes |
| Profit | 70 paise | 1 rupee |
The constraints are
4x + 6y ≤ 240
6 x + 3y ≤ 240
Total profit
z = 0.70 x + 1y
∴l.P.P is
maximise z = 0.7 x + y
subject to,
2x +3y ≤ 120
2x + y ≤ 80
x ≥0, y ≥0
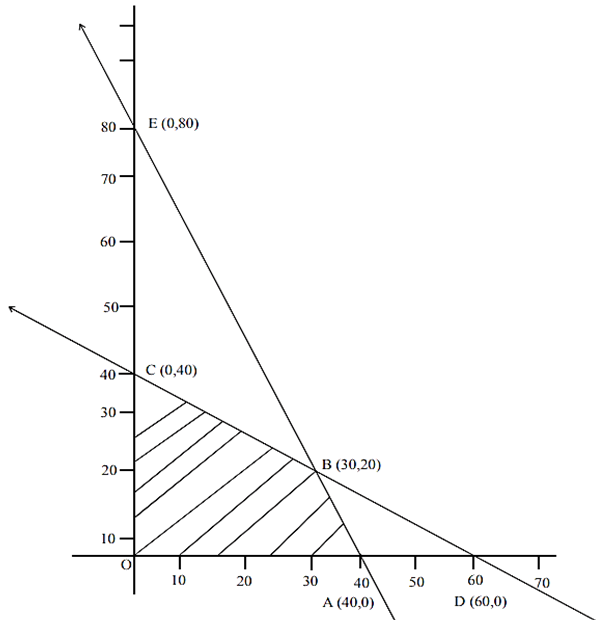
∴ common feasible region is OCBAO
| Correct point | Z = 0.7x + y |
| A (40,0) | Z(A) = 28 |
| B (30,20) | Z (B) = 41 maximum |
| C (0,40) | Z(C) = 40 |
| O(0,0) | Z(O) = 0 |
The maximum value of 'Z' is 41 at (30,20). Thus the factory showed produce 30 packages at screw A and 20 packages of screw B to ge the maximum profit of Rs.41
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
Let the land allocated for crop A be x hectares and crop B be y hectares.
Maximum area of the land available for two crops is 50 hectares. 
Liquid herbicide to be used for crops A and B are at the rate of 20 litres and 10 litres per hectare respectively. Maximum amount of herbicide to be used is 800 litres. 
The profits from crops A and B per hectare are Rs 10,500 and Rs 9,000 respectively.
Thus, total profit = Rs (10,500x + 9,000y) = Rs 1500 (7x + 6y)
Thus, the linear programming problem is:
Maximize Z = 1500 (7x + 6y) subject to the constraints
The feasible region determined by constraints is represented by the shaded region in the following graph:
The corner points of the feasible region are O (0, 0), A (40, 0), B (30, 20) and C (0, 50). The value of Z at these corner points are
| Corner point | Z = 1500 (7x+6y) | |
| O(0, 0) | 0 | |
| A (40, 0) | 420000 | |
| B (30, 20) | 495000 | Maximum |
| C (0, 50) | 450000 |
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Maximize Z = 0.1x + 0.09 y
x + y ≤ 50000
x ≥ 20000
y ≥ 10000
y ≤ x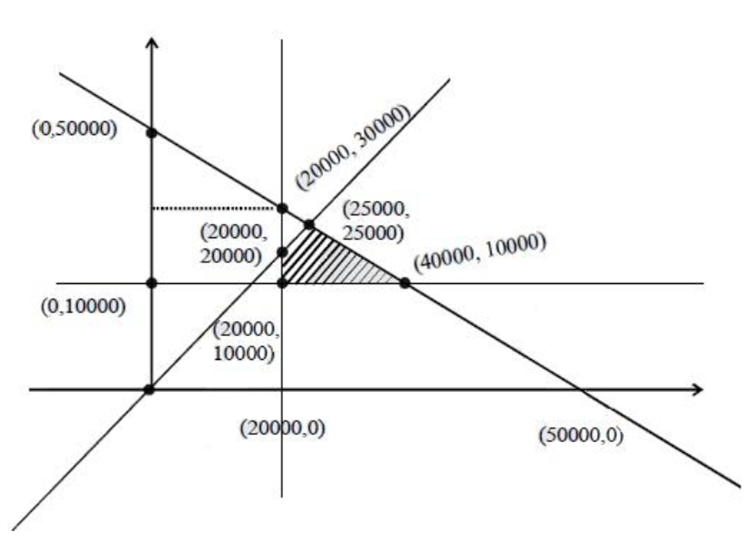
|
|
z=0.1 x+0.09y |
|
P1 (20000,10000) |
2900 |
|
P2(40000,10000) |
4900 |
|
P3(25000,25000) |
4750 |
|
P4(20000,20000) |
3800 |
Minimum and maximum z = 5x + 2y subject to the following constraints:
x – 2y ≤ 2
3x + 2y ≤ 12
−3x + 2y ≤ 3
x ≥ 0, y ≥ 0


| Point (x,y) | Values of the objective function Z= 5x+2y |
| A(0, 5) | 5 × 0 + 2 × 5 = 10 |
| B(3.5, 0.75) | 5 x 3.5 +2 x 0.75 =19 (Maximum) |
| C(2, 0) | 5 x 1.5 +2 x 3.75 =15 |
| O(0,0) | 5 x 0 + 2 x 0 = 0 (Minimum) |
