If a line makes angles 90°, 135°, 45° with x, y and z-axes re
    • Zigya Logo

    Three Dimensional Geometry
    pdf download
    zigya tab

    Show that  the points (2, 3, 4), (–1, –2, 1), (5, 8, 7) are collinear.

    Let P (2, 3, 4), Q (–1, –2, 1), R (5, 8, 7) be given points.
    The direction ratios of PQ are –1, –2, –2 –3, 1 – 4 i.e. – 3, – 5, – 3
    The direction ratios of PR are 5 – 2, 8 – 3, 7 –4 i.e. 3, 5, 3
    Since fraction numerator negative 3 over denominator 3 end fraction equals space fraction numerator negative 5 over denominator 5 end fraction equals fraction numerator negative 3 over denominator 3 end fraction
    ∴    lines PQ and PR are parallel.
    But P is a common point on both the lines points
    ∴    P, Q, R are collinear.
    119 Views
    Answer
    Find the direction cosines of the sides of the triangle whose vertices are (3, 5, –4), (–1, 1, 2) and (–5, –5, –2).
    Let A(3, 5, – 4), B(–1, 1, 2), C(–5, –5, –2) be the vertices of ΔABC.
    Direction ratios of AB are – 1 – 3, 1 – 5, 2 + 4 i.e. – 4, – 4, 6
              Dividing each by square root of left parenthesis negative 4 right parenthesis squared plus left parenthesis negative 4 right parenthesis squared plus left parenthesis 6 right parenthesis squared end root
    equals space square root of 16 plus 16 plus 36 end root space equals space square root of 68 comma space we space get space the space direction space
    cosines of the line AB as negative fraction numerator 4 over denominator square root of 68 end fraction comma space minus fraction numerator 4 over denominator square root of 68 end fraction comma space fraction numerator 6 over denominator square root of 68 end fraction
        i.e.       negative fraction numerator 1 over denominator square root of 17 end fraction comma space space space minus fraction numerator 2 over denominator square root of 17 end fraction comma space fraction numerator 3 over denominator square root of 17 end fraction.


    Direction ratios of BC are – 5 + 1, –5 –1, –2 –2 i.e. – 4, –6, –4.
                   Dividing each by square root of left parenthesis negative 4 right parenthesis squared plus left parenthesis negative 6 right parenthesis squared plus left parenthesis negative 4 right parenthesis squared end root space equals space square root of 16 plus 36 plus 16 end root space equals space square root of 68 comma space we space get space the space     
               direction ratios of the line BC as negative fraction numerator 4 over denominator square root of 68 end fraction comma space minus fraction numerator 6 over denominator square root of 68 end fraction comma space minus fraction numerator 4 over denominator square root of 68 end fraction space space space or space space space minus fraction numerator 2 over denominator square root of 17 end fraction comma space minus fraction numerator 3 over denominator square root of 17 end fraction comma space minus fraction numerator 2 over denominator square root of 17 end fraction.
      Direction ratios of CA are 3+5, 5+5,  -4+2 i.e., 8, 10 -2.

      Dividing each by square root of left parenthesis 8 right parenthesis squared plus left parenthesis 10 right parenthesis squared plus left parenthesis negative 2 right parenthesis squared end root space equals space square root of 64 plus 100 plus 4 end root space equals space square root of 168 comma space we space get space the space
    direction ratios of the line CA as fraction numerator 8 over denominator square root of 168 end fraction comma space fraction numerator 10 over denominator square root of 168 end fraction comma space space minus fraction numerator 2 over denominator square root of 168 end fraction comma space straight i. straight e. space fraction numerator 4 over denominator square root of 42 end fraction comma space fraction numerator 5 over denominator square root of 42 end fraction comma space minus fraction numerator 1 over denominator square root of 42 end fraction.
    145 Views
    Answer

    Find the cartesian equation of the line which passes through the point (-2, 4, -5) and is parallel to the line given by fraction numerator straight x plus 3 over denominator 3 end fraction space equals space fraction numerator straight y minus 4 over denominator 5 end fraction space equals fraction numerator straight z plus 8 over denominator 6 end fraction

    Direction-ratios of the line fraction numerator straight x plus 3 over denominator 3 end fraction space equals fraction numerator straight y minus 4 over denominator 5 end fraction space equals fraction numerator straight z plus 8 over denominator 6 end fraction space space are space 3 comma space 5 comma space 6.
    ∴     equation of the line through (–2, 4, –5) and having direction ratios 3, 5, 6 are
    fraction numerator straight x plus 2 over denominator 3 end fraction space equals fraction numerator straight y minus 4 over denominator 5 end fraction space equals fraction numerator straight z plus 8 over denominator 6 end fraction

    109 Views
    Answer
    Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

    Let P (1, –1, 2), Q (3, 4, –2), R (0, 3, 2) and S (3, 5, 6) be given points.
    Direction ratios of RS are 3 - 0, 5 - 3, 6 - 2 i.e. 3, 2, 4.
    ∴  direction cosines of RS are
            fraction numerator 3 over denominator square root of 9 plus 4 plus 16 end root end fraction comma space space fraction numerator 2 over denominator square root of 9 plus 4 plus 16 end root end fraction comma space fraction numerator 4 over denominator square root of 9 plus 4 plus 6 end root end fraction
    i.e.,    fraction numerator 3 over denominator square root of 29 end fraction comma space fraction numerator 2 over denominator square root of 29 end fraction comma space fraction numerator 4 over denominator square root of 29 end fraction
    Projection of PQ on RS
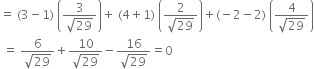
                               equals space left parenthesis 3 minus 1 right parenthesis space open parentheses fraction numerator 3 over denominator square root of 29 end fraction close parentheses plus space left parenthesis 4 plus 1 right parenthesis space open parentheses fraction numerator 2 over denominator square root of 29 end fraction close parentheses plus left parenthesis negative 2 minus 2 right parenthesis space open parentheses fraction numerator 4 over denominator square root of 29 end fraction close parentheses space equals space fraction numerator 6 over denominator square root of 29 end fraction plus fraction numerator 10 over denominator square root of 29 end fraction minus fraction numerator 16 over denominator square root of 29 end fraction equals 0

    ∴  PQ is perpendicular to RS
    Hence the result.

    117 Views
    Answer
    Advertisement
    Zigya App

    If a line makes angles 90°, 135°, 45° with x, y and z-axes respectively, find its direction cosines.

    Let l, m, n be the direction cosines of the line with direction angles 90°, 135°, 45°.
    therefore space space straight l space equals space cos space 90 degree space equals space 0 comma space space space straight m space equals space cos space 135 degree space equals space cos space left parenthesis 180 degree minus 45 degree right parenthesis space equals space minus cos space 45 degree space equals space minus fraction numerator 1 over denominator square root of 2 end fraction comma
               straight n space equals space cos space 45 degree space equals space fraction numerator 1 over denominator square root of 2 end fraction
    therefore space space   direction cosines are 0,  negative fraction numerator 1 over denominator square root of 2 end fraction comma space fraction numerator 1 over denominator square root of 2 end fraction.
    439 Views
  • zigya switch icon Switch
    • Advertisement
    Advertisement
    Flag Popup Icon
    Flag it
    Submit
    Flag Popup Icon
    Switch to
  • Type
  • Category
    • flexipad
    Share It Icon
    Share it
    Share It
    Share it