Given, 

$$\begin{gathered} \mathrm{Refracting} \mathrm{angle} \mathrm{of} \mathrm{prism}, \mathrm{A} = 60° \\ \mathrm{Angle} \mathrm{of} \mathrm{minimum} \mathrm{deviation}, \mathrm{\delta m} = 40° \end{gathered}$$ 
$\mathrm{Refractive} \mathrm{index} \mathrm{of} \mathrm{glass} \mathrm{w}.\mathrm{r}.\mathrm{t} \mathrm{air},{ }^{\mathrm{a}}{\mathrm{\mu }}_{\mathrm{g}} = \frac{\mathrm{Sin}{\displaystyle \frac{\left(\mathrm{A}+\mathrm{\delta m}\right)}{2}}}{\mathrm{SinA}/2}$ 
$\Rightarrow$          ${}_{\mathrm{a}}\mathrm{\mu }_{\mathrm{g}} = \frac{\sin 50°}{\sin 30°} = \frac{0.766}{0.54} = 1.532$ 

After the prism is placed in water, 

Refractive index of water = 1.33
Using the formula,

                ${}_{\mathrm{\omega }}\mathrm{\mu }_{\mathrm{g}} = \frac{\sin \left({\displaystyle \frac{\mathrm{A}+\mathrm{\delta }{\text{'}}_{\mathrm{m}}}{2}}\right)}{\mathrm{Sin} \mathrm{A}/2}$

              $\frac{{}^{\mathrm{a}}\mathrm{\mu }_{\mathrm{g}}}{{}^{\mathrm{a}}\mathrm{\mu }_w} = \frac{\sin \left({\displaystyle \frac{60+\mathrm{\delta }{\text{'}}_{\mathrm{m}}}{2}}\right)}{\sin 30°}$ 

$\sin \left(30°+\frac{\mathrm{\delta }{\text{'}}_{\mathrm{m}}}{2}\right) = \frac{1}{2}\times \frac{1.532}{1.33} = 0.5759$

$\Rightarrow$   $30°+\frac{\mathrm{\delta }{\text{'}}_{\mathrm{m}}}{2} = 35°10\text{'}$ 

$\therefore$        $\frac{\mathrm{A}+\mathrm{\delta }{\text{'}}_{\mathrm{m}}}{2}= {35}^{o}10\text{'}$ 
           $$\begin{gathered} A + \delta {\text{'}}_m = {70}^o {20}^{\text{'}} \\ \delta {\text{'}}_m = {70}^{o }{20}^{\text{'}} - A \\ = {70}^0{20}^{\text{'}} - {60}^o \end{gathered}$$

i.e.,     $\mathrm{\delta }{\text{'}}_{\mathrm{m}} = 10°20\text{'}.$

which is the reqiured angle of minimum deviation. 

Given,

$$\begin{gathered} \mathrm{Object} \mathrm{distance}, \mathrm{u} = -12 \mathrm{cm} \\ \mathrm{Focal} \mathrm{length}, \mathrm{f} = + 15 \mathrm{cm} \\ \mathrm{Size} \mathrm{of} \mathrm{the} \mathrm{object}, \mathrm{O} = 4.5 \mathrm{cm} \end{gathered}$$

Now using the mirror formula, 
                    $\boxed{\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} =\frac{1}{\mathrm{f}}}$ 
we have, 

             $$\begin{gathered} \frac{1}{\mathrm{v}} =\frac{1}{\mathrm{f}}-\frac{1}{\mathrm{u}} \\ =\frac{1}{15}+\frac{1}{12} \\ = \frac{4+5}{60} \\ = \frac{9}{60} \\ \therefore \mathrm{v} = 60/9 = 6.7 \mathrm{cm} \end{gathered}$$

∴ Image is formed at 6.7 cm at the back of the mirror ( because v is positive)
Now,
Magnification, $\boxed{\mathrm{m} = \frac{\mathrm{I}}{\mathrm{O}} = -\frac{\mathrm{v}}{\mathrm{u}}}$ 

$\therefore$                       $$\begin{gathered} \frac{\mathrm{I}}{4.5} = -\frac{6.7}{-12} \\ \mathrm{I} = \frac{6.7 \times 4.5}{12} \\ = 2.5 \mathrm{cm}. \end{gathered}$$ 

Hence, the image formed is erect, and of course virtual. 

As, needle is moved farther away from the mirror then as a result, image moves away from the mirror (upto F) and keeps on decreasing in size.

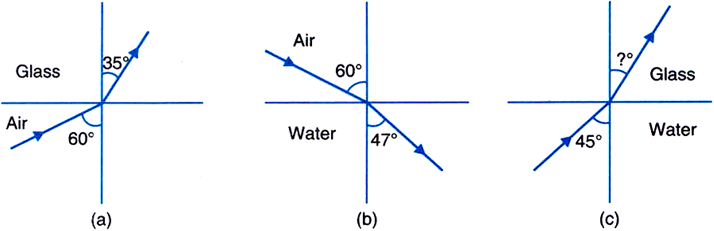
(a)
Given, 

$$\begin{gathered} \mathrm{Angle} \mathrm{of} \mathrm{incidence}, \mathrm{i} = 60° \\ \mathrm{Angle} \mathrm{of} \mathrm{refraction}, \mathrm{r} = 35° \end{gathered}$$ 

Using Snell's law, we have 

Refractive index of glass with respect to air,     ${}^{\mathrm{a}}\mathrm{\mu }_{\mathrm{g}} = \frac{\sin \mathrm{i}}{\sin \mathrm{r}} = \frac{\sin 60°}{\sin 35°}$

         $= \frac{0.8660}{0.5736} = 1.51$                                   

(b) 

$$\begin{gathered} \mathrm{Angle} \mathrm{of} \mathrm{incidence}, \mathrm{i} = 60° \\ \mathrm{Angle} \mathrm{of} \mathrm{refraction}, \mathrm{r} = 41° \end{gathered}$$ 

Using Snell's law, 

Refractive index of water wr.to air, ${}^{\mathrm{a}}\mathrm{\mu }_{\mathrm{w}} = \frac{\sin \mathrm{i}}{\sin \mathrm{r}} = \frac{\sin 60°}{\sin 41°} = 1.32$ 

(c)
Angle of incidence in water, $\mathrm{i} =45°$

Refractive index of glass wr.to water,
 ${}^{\mathrm{\omega }}\mathrm{\mu }_{\mathrm{g}} = \frac{{}^{\mathrm{a}}\mathrm{\mu }_{\mathrm{g}}}{{}^{\mathrm{a}}\mathrm{\mu }_{\mathrm{w}}} =\frac{\sin \mathrm{i}}{\sin \mathrm{r}}$
         $\frac{1.51}{1.32} = \frac{\sin 45°}{\sin \mathrm{r}} = \frac{0.7071}{\sin \mathrm{r}}$

$\therefore \sin \mathrm{r} = \frac{1.32 \times 0.7071}{1.51} = 0.6181$ 

$\Rightarrow$    $\mathrm{r} = 38.2°, which is the required angle of refraction of glass.$