What are the units of pressure?
Pressure represents force per unit area. The pressure expressed in terms of height of mercury column can be converted into the units of force per unit area.
Let a mercury column h cm high and A cm2 in ara of cross-section exert a downward force equal to the weight of mercury column. Therefore, per unit area of the surface is P.

where m = mass of mercury in the column
g = acceleration due to gravity
But mass = density x volume
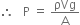
Where ρ and V represent density and volume of mercury respectively.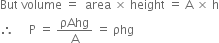
Standard atmospheric pressure. A standard pressure of one atmosphere (1 atm) is defined as the pressure exerted by a column of mercury 76 cm high at 273K (density of mercury is 13·595 g cm–3) and at standard gravity (i.e. 9·81 cm–2). That is,
1 atm = 76·0 cm of Hg = 760 mm of Hg = 760 torr.
The S.I. unit of pressure is pascal (Pa). It is defined as the pressure exerted when a force of 1 newton (1N) acts on a 1 m2 area. Pascal is related to atmosphere or bar as
1 bar =1 atm = 1 ·0133 × 105 Nm–2
= 1 ·0133 × 105 Pa = 101·33 k Pa
However, for approximate work,
1 bar 1 atm = 102 k Pa = 105 Pa
State Boyle's law. How this law is expressed mathematically?
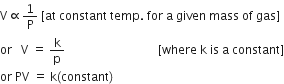
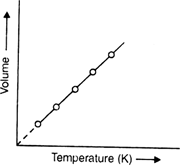
Charle's law states: Pressure remaining constant the volume of a given mass of gas increases or decreases by  volume at
volume at  for each one-degree rise or fall in temperature.
for each one-degree rise or fall in temperature.
Mathematically,
If V0 is the volume at 0°C, then the volume at various other temperatures can be written as:
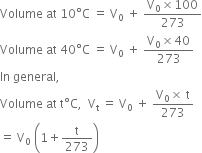
But if the gas is cooled to –273°C, then its volume becomes zero.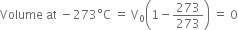
This implies that a gas at -273°C will have zero or no volume i.e. it will cease to exist. In actual practice, all gases liquefy before this temperature is reached. Also –273°C should be the lowest possible temperature because any further cooling would lead to a volume of less than zero or negative volume which is meaningless. Therefore, this temperature (–273° C) was termed as absolute zero of temperature.
Another statement of Charle’s law:
According to Charle’s law, volume of a given mass of a gas at different temperatures is related to its volume (V0) at 0°C as follows:
Volume at 
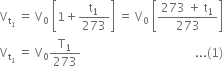
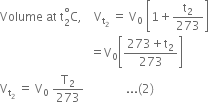
Dividing (1) by (2), we get,
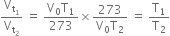
[Pressure and mass of the gas constant]
Hence Charle’s law may also be stated as Pressure remaining constant, the volume of a given mass of a gas is directly proportional to absolute temperature i.e. 
Thus, if V1 is the initial volume of the gas at temperature T1 (in degree kelvin) and V2 is the final volume of the gas at temperature T2 (in degree kelvin), keeping pressure constant, then
How will you represent the Boyle's law graphically in different ways?
This law can be represented in three ways:
(i) Graph between P (pressure) and V (volume):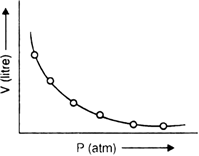
If a graph is plotted between P and V of gas at a particular temperature, a curve of the form of the regular hyperbola is obtained. This shows that volume is inversely proportional to pressure.
(ii) Graph between P (pressure) and  : (1/volume):
: (1/volume):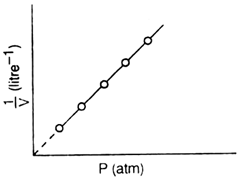
If a graph is plotted between P and 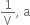
a straight line is obtained which shows that pressure and volume are inversely related to each other.
(iii) Graph between P(pressure) and PV (Product of pressure and volume):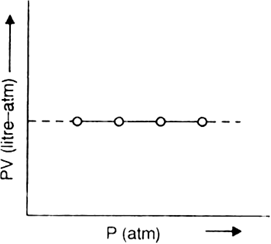
If a graph is plotted between P and PV, a horizontal straight line is obtained. This illustrates the relationship
PV = constant.
These curves plotted at particular temperature are known as isotherms.
How will you verify Charle's law graphically? What is the practical importance of Charle's law?