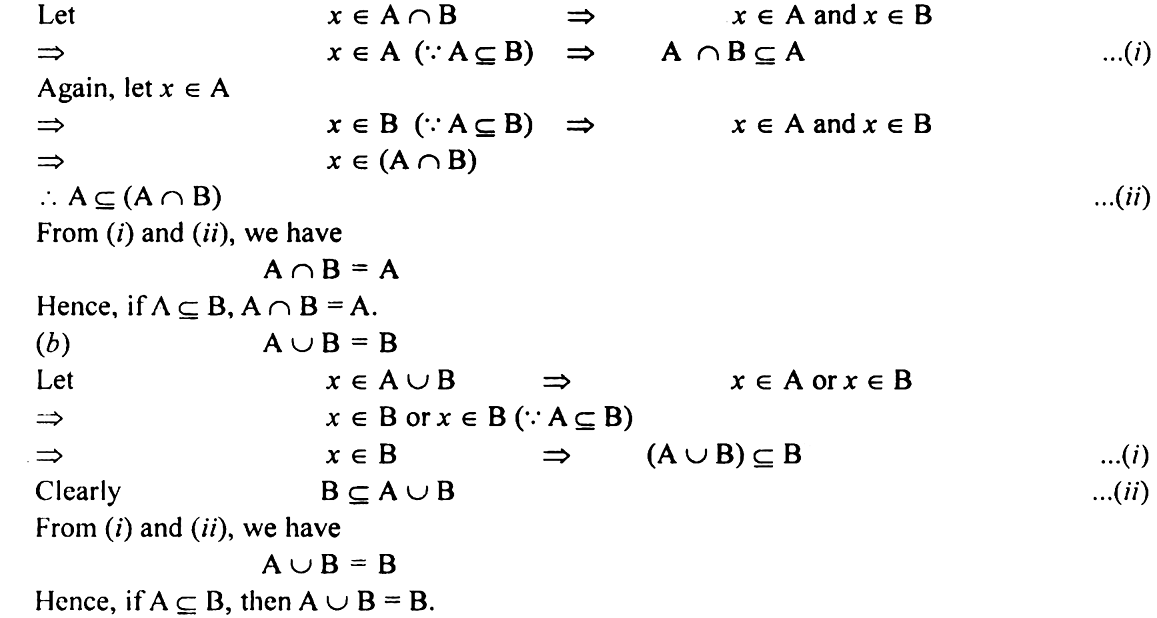Write the following sets in the roster form :
(i) A = {jt : x ∊ Z and x is a root of the quadratic equation x2 - 3x - 10 = 0}
(ii) B = {x : x ∊ N, -5 < x - 2 < 5}
(iii) C = {x : jc is an odd prime number less than 30}
(i) A = ![]() and x is a root of quadratic equation x2 -3x -10 = 0}
and x is a root of quadratic equation x2 -3x -10 = 0}
Now, x2 -3x -10 = 0 ![]() (x-5) (x+2) = 0
(x-5) (x+2) = 0![]() x=5, -2 which are both integers.
x=5, -2 which are both integers.
Hence, A = {-2, 5}
(ii) B= {x :x ![]() , -5 < x-2 < 5}
, -5 < x-2 < 5}
Now, -5 < x-2 < 5![]() -3 < x < 7
-3 < x < 7![]() x is a natural number between -3 and 7 (exclusive).
x is a natural number between -3 and 7 (exclusive).
Hence, B = {1, 2, 3, 4, 5, 6}
(iii) C = {x : x is an odd prime number less than 30}![]() x = 3, 5, 7, 11, 13, 17, 19, 23, 29
x = 3, 5, 7, 11, 13, 17, 19, 23, 29
Hence C = { 3, 5, 7, 11, 13, 17, 19, 23, 29}
Write the following intervals in set-builder form :
(i)-∞ 31 (ii) (-∞, 0) (iii) [-1, ∞) (iv) (3, ∞)

If A ⊆ B, show that:
(a) A ∩ B=A (b) A ∪ B = B