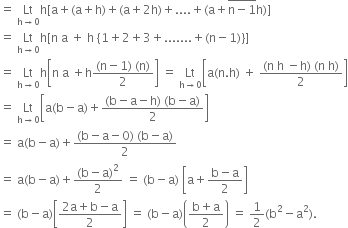CBSE
Gujarat Board
Haryana Board
Class 10
Class 12
Evaluate as the limit of a sum.
Comparing Now, =
Evaluate the following definite integrals as limit of sums.
Let I = Since by second fundamental theorem, I = F(3) - F(2) =
Comparing ......................................Now
Comparing Now
Comparing f(x) = x - 1, a = 0, b = 5Now
by second fundamental theorem,
as the limit of a sum.
Switch
as the limit of a sum.
