18 g glucose (C6H12O6 ) is added to 178.2 g water. The vapor pressure of water (in torr) for this aqueous solution is:
76.0
752.4
759.0
759.0
B.
752.4
Vapour pressure of water (p°) = 760 torr
Number of moles of glucose
Molar mass of water = 18 g/mol
Mass of water (given) = 178.2 g
Number of moles of water
Total number of moles = (0.1 +9.9) = 10 moles
Now, the mole fraction of glucose in solution = Change in pressure with respect to initial pressure.
therefore, Vapour pressure of solution = (760-7.6)torr
=752.4 torr
(a) Differentiate between molarity and molality for a solution. How does a change in temperature influence their values?
(b) Calculate the freezing point of an aqueous solution containing 10.50 g of MgBr2in 200 g of water. (Molar mass of MgBr2 = 184 g) (Kf for water = 1.86 K kg mol-1)
Molarity is defined as the number of moles of solute dissolved per liter of solution.

Molality of a solution is defined as the number of moles of solute dissolved in 1000 grams of solvent.

While molarity decreases with an increase in temperature, molality is independent of temperature. This happens because molality involves mass, which does not change with a change in temperature, while molarity involves volume, which is temperature dependent.
b) Given
w2 = 10.50 g
w1 = 200 g
Molar mass of MgBr2 (M2) = 184 g
Using the formula, 
(a) Define the terms osmosis and osmotic pressure. Is the osmotic pressure of a solution a colligative property? Explain.
(b) Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to 250.0 g of water. (Kb for water = 0.512 K kg mol-1), (Molar mass of NaCl = 58.44 g)
(a) Osmosis: The process of flow of solvent molecules from pure solvent to a solution or from a solution of lower concentration to a solution of higher concentration through a semi-permeable membrane is called osmosis.
Osmotic Pressure: The pressure required to just stop the flow of solvent due to osmosis is called osmotic pressure (π) of the solution.
Yes, the osmotic pressure of a solution is a colligative property. The osmotic pressure is expressed as.

Where,
π = osmotic pressure
n = number of moles of solute
V = volume of solution
T = temperature
From the equation, it is clear that osmotic pressure depends on upon the number of moles of solute ‘n’ irrespective of the nature of the solute.
Hence, osmotic pressure is a colligative property.
(b) Given
Kb = 0.512 k kg mol-1
w2 = 15.00 g
w1 = 250.0 g
M2 = 58.44 g
Using the formula, 
(a) State Raoult’s law for a solution containing volatile components.
How does Raoult’s law become a special case of Henry’s law?
(b) 1·00 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0·40 K. Find the molar mass of the solute. (Kf for benzene = 5·12 K kg mol-1)
(a) Let p1, p2 = Partial vapour pressure of two volatile components 1 and 2 of a mixture ![]()
= Vapour pressure of pure components 1 and 2
x1, x2 = Mole fractions of the components 1 and 2
ptotal = Total vapour pressure of the mixture then Raoult’s law can be stated as: For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
That is, for component 1,
p1 ![]() x1
x1
And, p1 = ![]() x1
x1
For component 2,
P2 = ![]() x2
x2
According to Dalton’s law of partial pressures,
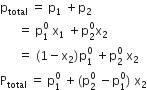
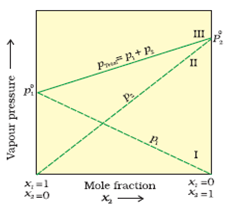
The plot of vapour pressure and mole fraction of an ideal solution at constant temperature is shown below.
Raoult’s Law as a Special Case of Henry’s Law
According to Raoult’s law, the vapour pressure of a volatile component in a given solution is p1 =![]() x1
x1
According to Henry’s law, the partial vapour pressure of a gas (the component is so volatile that it exists as gas) in a liquid is
p = KH x
It can be observed that in both the equations, the partial vapour pressure of the volatile component varies directly with its mole fraction. Only the proportionality constants KH and are different. Thus, Raoult’s law becomes a special case of Henry’s law in which KH is equal to .
(b) Given: w2 = 1g (weight of solute)
w1 = 50 g (weight of solvent)
Tf = 0.40 K
kf = 5.12 K Kg mol-1
M2 =? (Molar mass of solute)
Using the equation,
Tf = Kfm (where m is molality)
0.40 = 5.12 x m
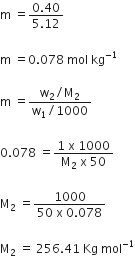
(a) Define the following terms:
(i) Ideal solution
(ii) Azeotrope
(iii) Osmotic pressure
(b) A solution of glucose (C6H12O6) in water is labeled as 10% by weight. What would be the molality of the solution?
(Molar mass of glucose = 180 g mol-1)
(a)
(i) Ideal Solution:
Solutions which obey Raoult’s law over the entire range of concentrations are known as the ideal solution. Along with that for ideal solution:
Enthalpy of mixing of the pure components to form the solution i.e  mix H = 0 and volume of mixing,
mix H = 0 and volume of mixing,  mix V = 0.
mix V = 0.
An ideal solution will be formed when intermolecular forces of attraction between the molecules of solute (A - A) and those between the molecules of solvent (B -B) are nearly equal to those between solute and solvent molecules (A - B).
For Example n-Hexane and n-heptane
(ii) Azeotropes
Binary mixtures which have the same composition in liquid and vapour phase, and have constant boiling points are known as azeotropes. It is not possible to separate its components by fractional distillation .There are two types of azeotropes:
Minimum boiling azeotrope, example: Ethanol-water mixture containing ethanol approximately 95% by volume.
Maximum boiling azeotrope, example: Nitric acid-water mixture containing 68% nitric acid and 32% water by mass.
(iii) Osmotic Pressure
The process of flow of solvent molecules from pure solvent to a solution or from a solution of lower concentration to a solution of higher concentration through a semi-permeable membrane is called osmosis. The pressure required to prevent the flow of solvent due to osmosis is called osmotic pressure (Ï€) of the solution.
Osmotic pressure is directly proportional to the molarity C of the solution at a given temperature T.

Where,
n2 = Number of moles of solute
V= Volume of the solution in litres
(b) Assume that 100 g of solution contains 10 g of glucose and 90 g of water as our glucose solution is 10% by weight
Where w2 = weight is solute in 'g'
w1 = weight of solvent in 'g'
M2 = Molecular mass of solute.
So,
