
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when edge is 10 cm long?
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Let r cm be the radius of the circle.
From given condition, rate of increase = 3 cm per second![]()
Let A be the area of circle, ![]()
![]()
![]()
![]()
When r = 10, rate of increase of area = ![]()
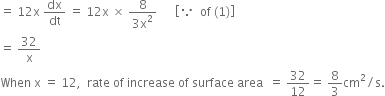
Tips: -
Since the rate of change is represented by derivative with respect to time, it is taken to be positive if the quantity is increasing and negative if the quantity is decreasing.