
2 किग्रा. सेब और 1 किग्रा. अंगूर का मूल्य किसी दिन 160 रु. था एक महीने बाद 4 किग्रा. सेब और 2 किग्रा. अंगूर का मूल्य 300 रु. हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
माना एक किग्रा.सेब का क्रय मूल्य = x रु.
माना एक किग्रा. अंगूर का मूल्य = y रु.
प्रश्नानुसार
2x + y = 160 ...( i )
4x + 2y = 300
⇒ 2x + y = 150 ... ( ii )
2x + y = 160
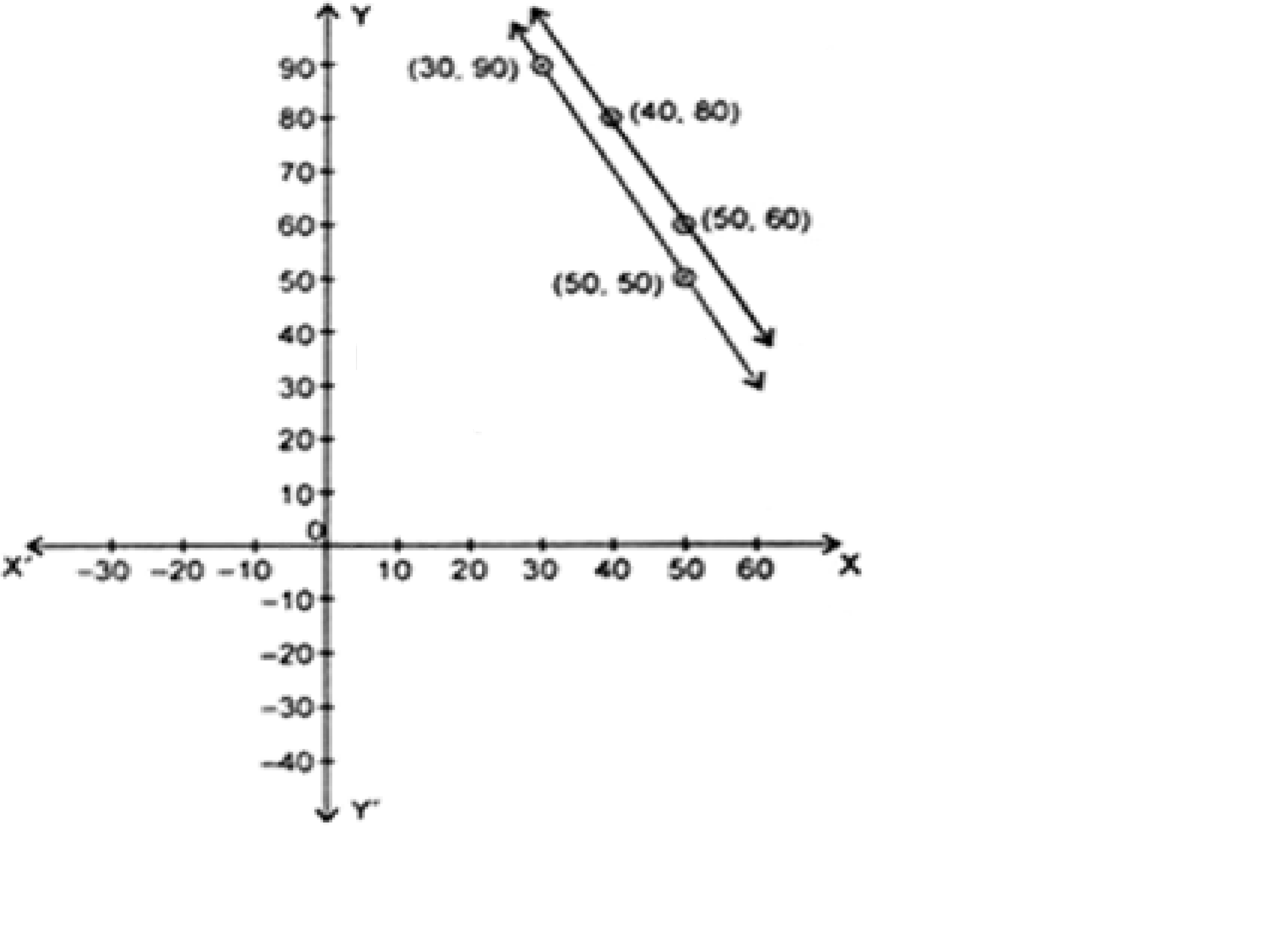
⇒ y = 160 - 2x![]()
2x + y = 150
⇒ y = 150 - 2x![]()
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफ़िय विधि से हल ज्ञात कीजिए:
5 पेंसिल तथा 7 कलमों का कुल मूल्य 50 रु. है, जबकि 7 पेंसिल तथा 5 कलमों का कुल मूल्य 46 रु. है। एक पेंसिल तथा एक कलम का मूल्य ज्ञात कीजिए।
माना एक पेंसिल का मूल्य = x
माना एक कलम का मूल्य = y
5 पेंसिल का मूल्य = 5x
7 कलम का मूल्य = 7y
प्रश्नानुसार,
5x + 7y = 50
7x + 5y = 46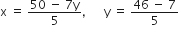
| x | 10 | 3 |
| y | 0 | 5 |
| x | 3 | - 2 |
| y | 5 | 12 |
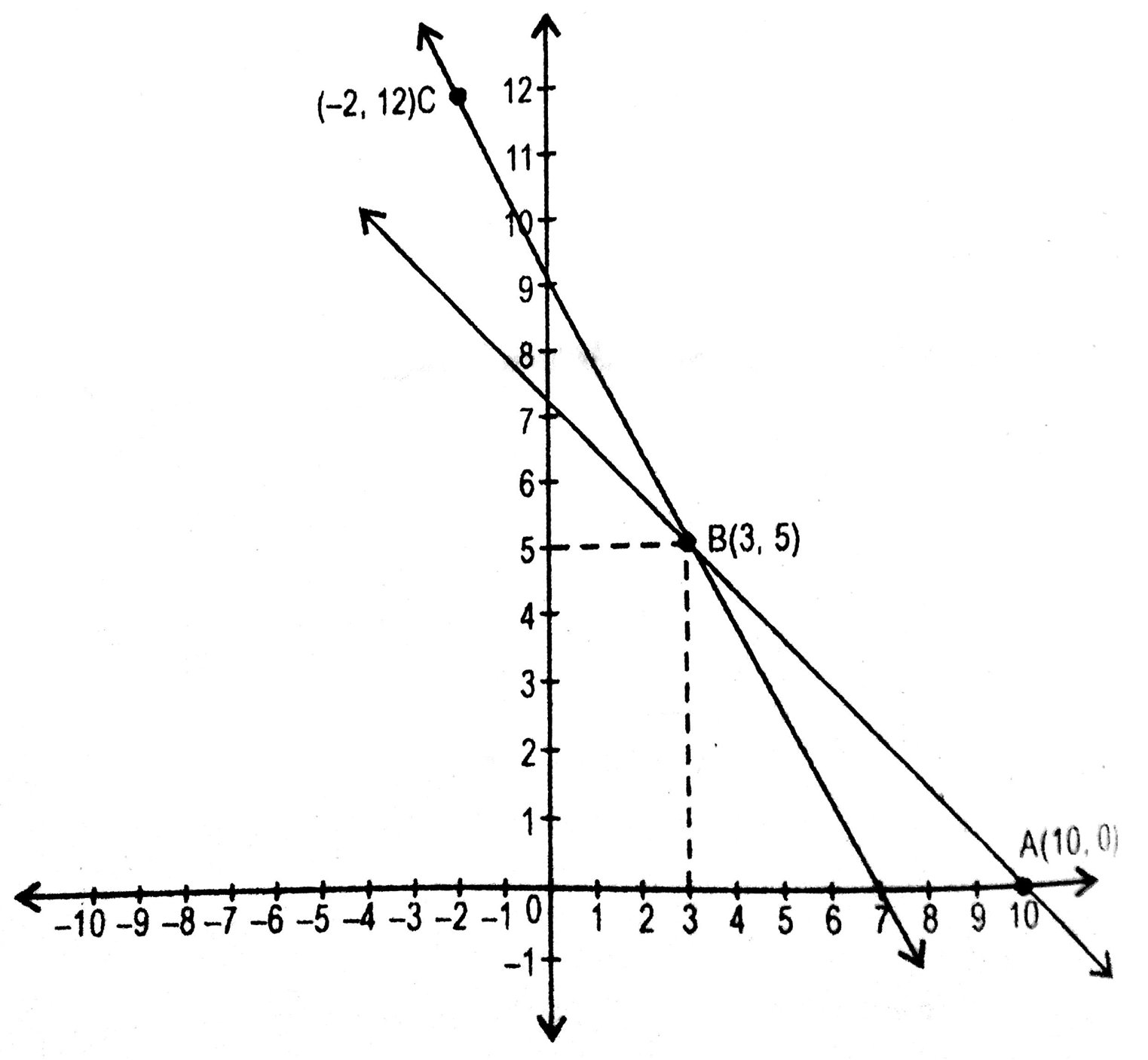
इन बिंदुओं को मिलाने पर हमें दो सरल रेखाएं प्राप्त होती हैं जो एक दूसरे को बिंदु B ( 3, 5 ) पर काटती है।
इसलिए x = 3 और y = 5 रैखिक समीकरणों का अभीष्ट हल है।
क्रिकेट टीम के एक कोच ने 3900 रु. में 3 बल्ले तथा 6 गेंदे खरीदीं। बाद में उसने एक और बल्ला तथा उसी प्रकार की 2 गेंदे 1300 रु. में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
माना एक बल्ले का मूल्य = x
माना एक गेंद का मूल्य = y
3 बल्लों का मूल्य = 3x
6 गेंदों का मूल्य = 6y
प्रश्नानुसार
3x + 6y = 3900
एक बल्ले का मूल्य = x
3 गेंदों का मूल्य = 3y
प्रश्नानुसार
x + 3y = 1300
3x + 6y = 3900 ...( i )
x + 3y = 1300 ...( ii )
3x + 6y = 3900
⇒ 3( x + 2y ) = 3900
⇒ x + 2y = 1300
⇒ x = 1300 - 2y![]()
x + 3y = 1300
x = 1300 - 3y

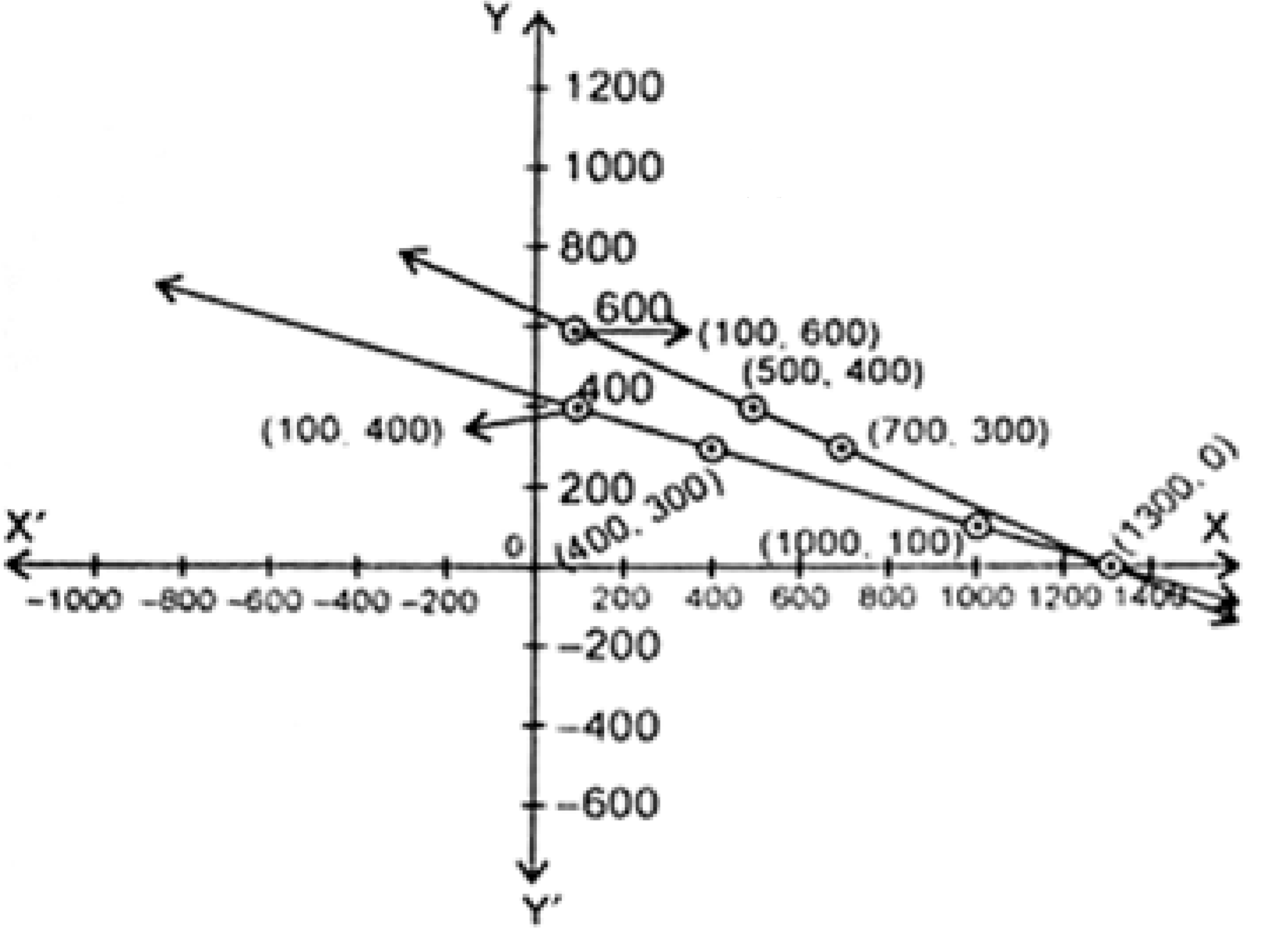
अफ़ताब अपनी पुत्री से कहता है, 'सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।' ( क्या यह मनोरंजक है? ) इस स्थिति को बीजगणितीय एवं ग्राफ़िय रूपों में व्यक्त कीजिए।
माना बेटी की वर्तमान आयु = x वर्ष
माना पिता की वर्तमान आयु = y वर्ष
सात वर्ष पहले, बेटी की आयु = x - 7 वर्ष
पिता की आयु = y - 7 वर्ष
तीन वर्ष बाद, बेटी की आयु = x + 3 वर्ष
पिता की आयु = y + 3 वर्ष
प्रश्नानुसार,
y - 7 = 7 ( x - 7 )
y - 7 = 7x - 49
7x - y = 42 ... ( i )
y + 3 = 3 ( x + 3 )
y + 3 = 3x + 9
3x - y = - 6 ... ( ii )
समीकरणों से
y = 7x - 42
| x | 6 | 7 |
| y | 0 | 7 |
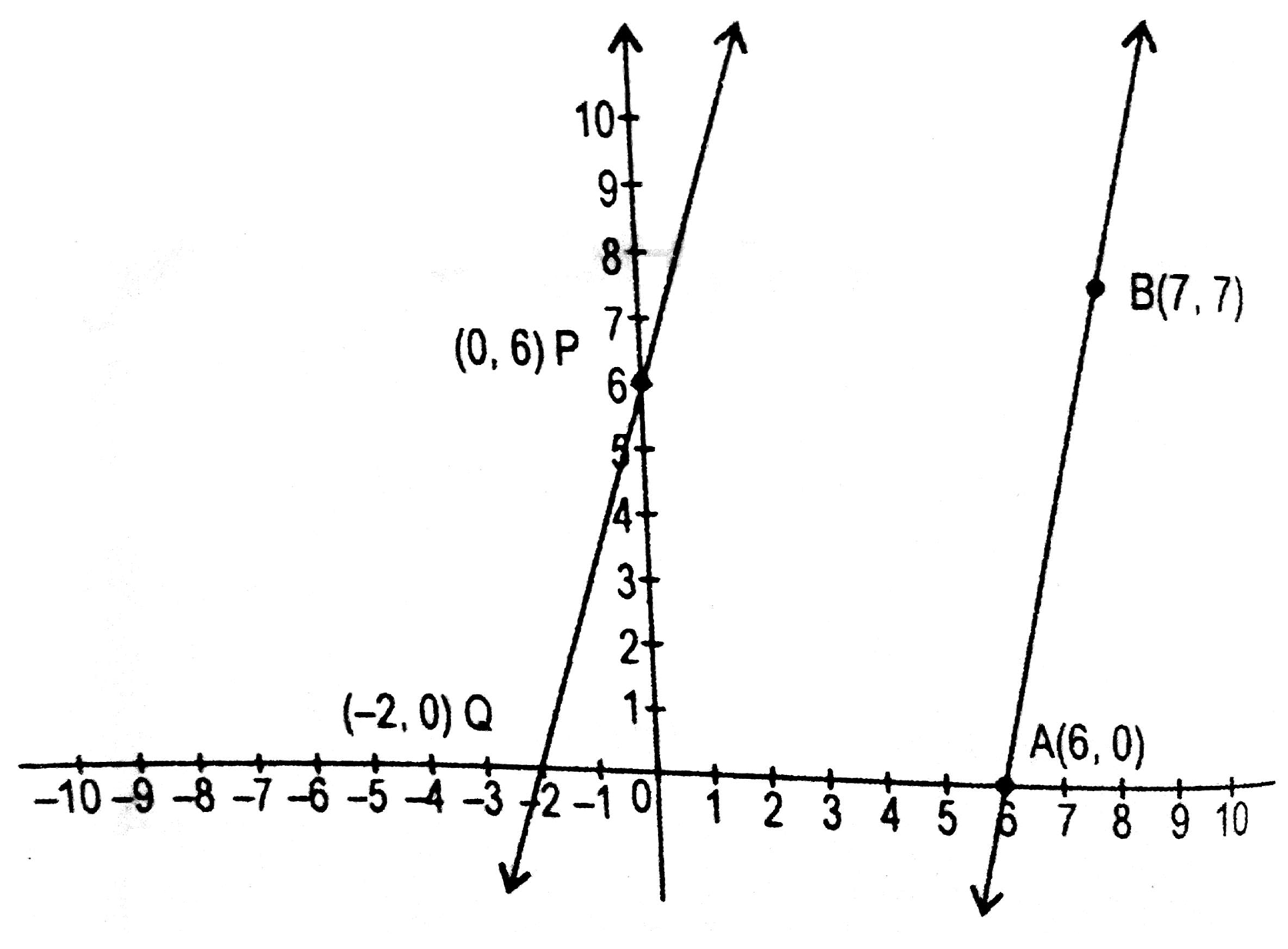
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफ़िय विधि से हल ज्ञात कीजिए:
( i ) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
माना लड़कों की संख्या = x, और लड़किओं की संख्या = y
x + y = 10 ...(i)
y = x + 4
⇒ x - y = - 4 ...(ii)
x + y = 10
⇒ x = 10 - y
x - y = - 4
⇒ x = y - 4

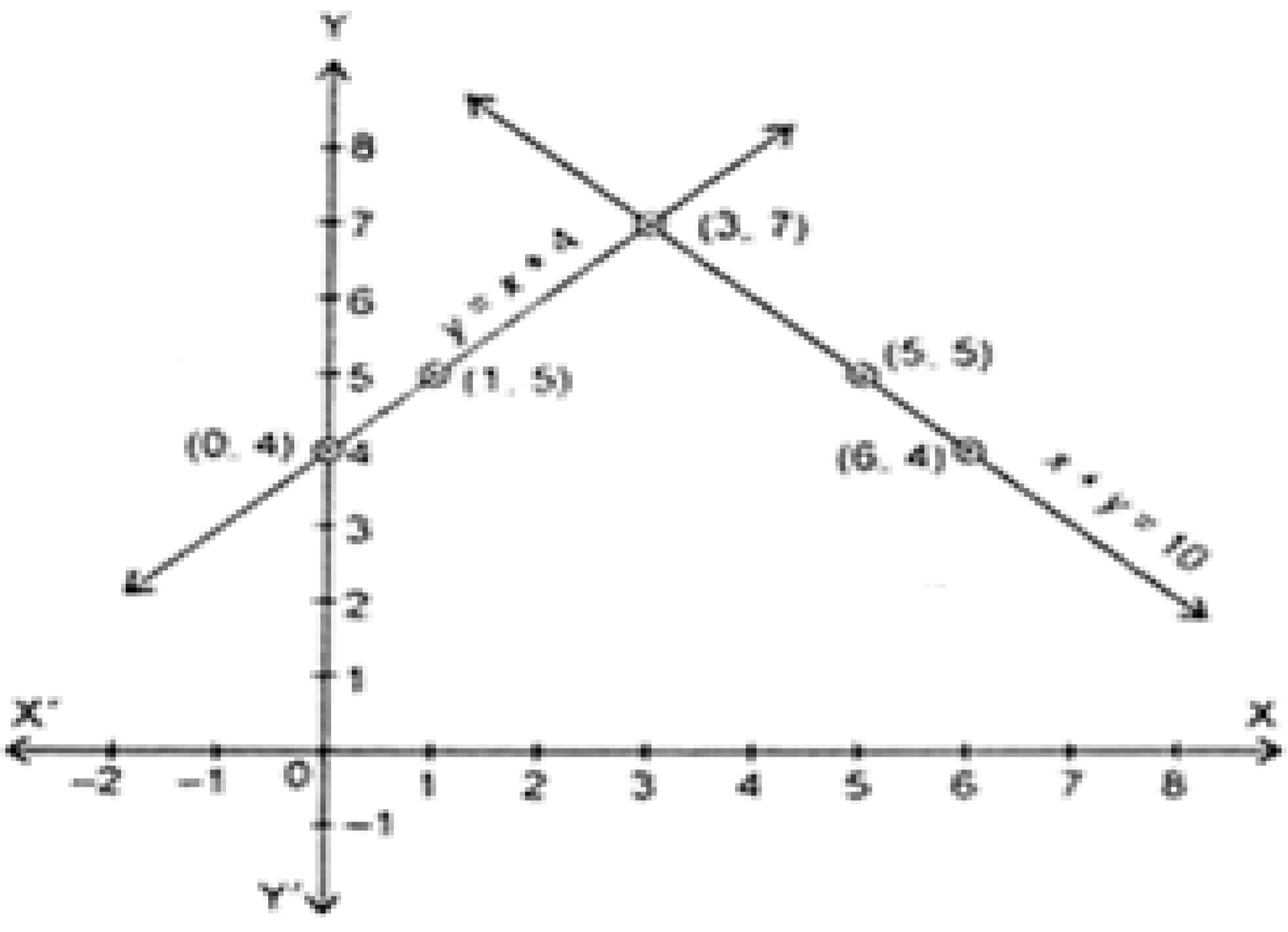
बिंदुओं को मिलाने पर दो सरल रेखाएँ प्राप्त होती है जो एक दूसरे को ( 3, 7 ) पर काटती है इसलिए x = 3 और y = 7 रैखिक समीकरणों का अभीष्ट हल है।
लड़कों की संख्या = 3
लड़कियों की संख्या = 7
