Let  'a'  be the first term and  'd'  be the common difference of given  A.P.

Now,

4^th term = 22

$\Rightarrow$ a + 3 d = 22        ............( i )

15^th term = 66

$\Rightarrow$ a + 14 d = 66      ............( ii )

Subtracting  ( i )  from  ( ii ),  we have

11 d = 44

$\Rightarrow$ d = 4

Substituting the value of  'd'  in  ( i ),  we get

a = 22 - 3 x 4 

   = 22 - 12

   = 10

$\Rightarrow$ First term = 10.

Now,

$\mathrm{Sum} \mathrm{of} \mathrm{n} \mathrm{terms} = \frac{\mathrm{n}}{2} \left[ 2 \mathrm{a} + ( \mathrm{n} - 1 ) \mathrm{d} \right]$

$$\begin{gathered} \mathrm{Sum} \mathrm{of} 8 \mathrm{terms} = \frac{8}{2} \left[ 2 \times 10 + ( 8 - 1 ) \times 4 \right] \\ = \frac{8}{2} \left[ 2 \times 10 + 7 \times 4 \right] \\ = 4 \left[ 20 + 28 \right] \\ = 4 \times 48 \\ = 192 \end{gathered}$$

( k - 3 ),  ( 2 k + 1 )  and  ( 4 k + 3 )  are three consecutive terms of an A.P.

$\Rightarrow$ 2 ( 2 k + 1 ) = ( k - 3 ) + ( 4 k + 3 )

$\Rightarrow \; 4\; k\; +\; 2\; =\; k\; -\; 3\; +\; 4\; k\; +\; 3$

$\Rightarrow \; 4\; k\; +\; 2\; =\; 5\; k$

$\Rightarrow \; k\; =\; 2$

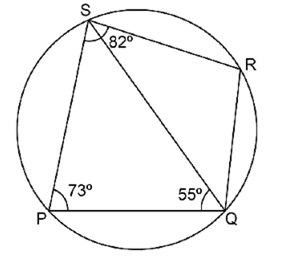
Given: PQRS is cyclic quadrilateral.

$\angle \mathrm{QPS} = 73° , \angle \mathrm{PQS} = 55° , \angle \mathrm{PSR} = 82°$

( i ) Opposite angle of a cyclic quadrilateral are supplementary.

$$\begin{gathered} \Rightarrow \angle \mathrm{QPS} + \angle \mathrm{QRS} = 180° \\ \Rightarrow 73° + \angle \mathrm{QRS} = 180° \\ \Rightarrow \angle \mathrm{QRS} = 180° - 73° = 107° \end{gathered}$$

( ii ) Opposite angle of a cyclic quadrilateral are supplementary.

$$\begin{gathered} \Rightarrow \angle \mathrm{PSR} + \angle \mathrm{PQR} = 180° \\ \Rightarrow \angle \mathrm{PSR} + ( \angle \mathrm{PQS} + \angle \mathrm{RQS} ) = 180° \\ \Rightarrow 82° + 55 + \angle \mathrm{RQS} = 180° \\ \Rightarrow \angle \mathrm{RQS} = 180° - 55° - 82° \\ \Rightarrow \angle \mathrm{RQS} = 43° \end{gathered}$$

( iii ) In $∆ \mathrm{PQS}$,  by angle sum property, we have 

$$\begin{gathered} \Rightarrow \angle \mathrm{PSQ} + \angle \mathrm{PQS} + \angle \mathrm{QPS} = 180° \\ \Rightarrow \angle \mathrm{PSQ} + 55° + 73° = 180° \\ \Rightarrow \angle \mathrm{PSQ} = 180° - 128° \\ \Rightarrow \angle \mathrm{PSQ} = 52° \\ \mathrm{Now}, \angle \mathrm{PRQ} = \angle \mathrm{PSQ} ( \mathrm{Angles} \mathrm{in} \mathrm{the} \mathrm{same} \mathrm{segment} \mathrm{of} \mathrm{a} \mathrm{circle} ) \\ \Rightarrow \angle \mathrm{PRQ} = 52° \end{gathered}$$