Let the number of cones be  n.

Let the radius of the sphere be  r_s = 6 cm

Radius of a cone be  r_c = 2 cm

And height of the cone be  h = 3 cm

Volume of sphere = n ( Volume of a metallic cone )

Hence, the number of cones is  72.

Length of the rectangle  =  Radius of two semi-circles  +  Diameter of a circle

                                    =  5 + 5 + 10 

                                    =  20 cm.

Breadth of rectangle  = Diameter of a circle = 2 x 5 = 10 cm.

$\therefore$ Area of a rectangle = Length  x Breadth

                                 = 20  x  10

                                 = 200  sq. cm

$$\begin{gathered} \mathrm{Area} \mathrm{of} \mathrm{a} \mathrm{circle} = \frac{22}{7} \times 5 \times 5 \\ = 78.571 \mathrm{sq}.\mathrm{cm} \\ \mathrm{And}, \mathrm{area} \mathrm{of} \mathrm{two} \mathrm{semi}-\mathrm{circles} \mathrm{each} \mathrm{of} \mathrm{radius} 5 \mathrm{cm} = 2 \left( \frac{1}{2} \times 78.571 \right) \\ = 78.571 \mathrm{sq}.\mathrm{cm} \end{gathered}$$

Now,

Area of shaded region  =  Area of a rectangle  -  Area of a circle  -  Area of a two semi-circles 

                                 =  200  -  78.571 - 78. 571

                                 =  200  -  157.142

                                 =  42.858  sq. cm.

$$\begin{gathered} - 3 ( \mathrm{x} - 7 ) \ge 15 - 7 \mathrm{x} > \frac{\mathrm{x} + 1}{3} \\ \Rightarrow - 3 ( \mathrm{x} - 7 ) \ge 15 - 7 \mathrm{x} \mathrm{and} 15 - 7 \mathrm{x} > \frac{\mathrm{x} + 1}{3} \\ \Rightarrow - 3 \mathrm{x} + 21 \ge 15 - 7 \mathrm{x} \mathrm{and} 45 - 21 \mathrm{x} > \mathrm{x} + 1 \\ \Rightarrow - 3 \mathrm{x} + 7 \mathrm{x} \ge 15 - 21 \mathrm{and} 45 - 1 > \mathrm{x} + 21 \mathrm{x} \\ \Rightarrow 4 \mathrm{x} \ge - 6 \mathrm{and} 44 > 22 \mathrm{x} \\ \Rightarrow \mathrm{x} \ge \frac{- 3}{2} \mathrm{and} 2 > \mathrm{x} \\ \Rightarrow \mathrm{x} \ge - 1.5 \mathrm{and} 2 > \mathrm{x} \\ \mathrm{The} \mathrm{solution} \mathrm{set} \mathrm{is} \left\{ \mathrm{x} : \mathrm{x} \in \mathrm{R}, - 1.5 \le \mathrm{x} < 2 \right\}. \end{gathered}$$

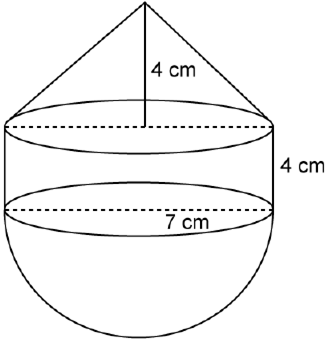
Volume of solid = Volume of cone + Volume of cylinder + Volume of hemisphere

$$\begin{gathered} Volume of cone = \frac{\mathrm{\pi } {\mathrm{r}}^2 \mathrm{h}}{3} \\ = \frac{22 \times 7 \times 7 \times 4}{7 \times 3} \\ = \frac{616}{3} c{m}^3 \\ Volume of cylinder = \mathrm{\pi } {\mathrm{r}}^2 \mathrm{h} \\ = \frac{22 \times 7 \times 7 \times 4}{7 } \\ = 616 {\mathrm{cm}}^3 \\ \mathrm{Volume} \mathrm{of} \mathrm{hemisphere} = \frac{2}{3} \mathrm{\pi } {\mathrm{r}}^3 \\ = \frac{2 \times 22 \times 7 \times 7 \times 7}{3 \times 7 } \\ = \frac{2156}{3} {\mathrm{cm}}^3 \\ \mathrm{Total} \mathrm{volume} = \frac{616}{3} + 616 + \frac{2156}{3} \\ = 1540 {\mathrm{cm}}^3 \end{gathered}$$

Let  h  be the height and  r  be the radius of the base of the conical tent.

Accordingto the given information,

$$\begin{gathered} 77 \times 16 = \frac{1}{3} \mathrm{\pi } {\mathrm{r}}^2 \mathrm{h} \\ \Rightarrow 77 \times 16 = \frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times \mathrm{h} \\ \Rightarrow 77 \times 16 = \frac{1}{3} \times 22 \times 7 \times \mathrm{h} \\ \Rightarrow \mathrm{h} = \frac{ 77 \times 16 \times 3}{22 \times 7 } \\ \Rightarrow \mathrm{h} = 24 \mathrm{m}. \\ \mathrm{Now}, {\mathrm{l}}^2 = {\mathrm{r}}^2 + {\mathrm{h}}^2 \\ \Rightarrow {\mathrm{l}}^2 = 7^2 + {24}^2 = 625 \\ \Rightarrow \mathrm{l} = 25 \mathrm{m}. \end{gathered}$$

$$\begin{gathered} \therefore \mathrm{Curved} \mathrm{surface} \mathrm{area} = \mathrm{\pi } \mathrm{r} \mathrm{l} \\ = \frac{22}{7} \times 7 \times 25 \\ = 550 {\mathrm{m}}^2 \end{gathered}$$

Hence, the height of the tent is  24 m  and the curved surface area of the tent is  550 m².