The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is and respectively.

Find the height of the two towers. Give your answer correct to 3 significant figures.
Consider the following figure:

In ,
In ,
Thus, the height of first tower, AB = AE + EB
= 69.282 + 53.427
= 122.709m = 122 m
And height of second tower, CD = EB = 53.427m = 53.4m
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Let consider A be the position of the aeroplane and let BC be the river. Let D be the point in BC just below the aeroplane.

For ΔADC, we get
For ΔADB, we get
Therefore, the width of the river is DB + DC = 250 + = 394m.
The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 600 and 450 respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships, Give your answer correct to the nearest whole number.
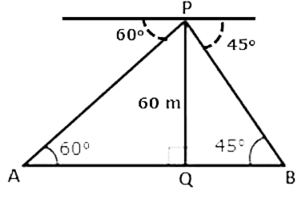
Let PQ be the light house.
= 20 x 1.732 + 60
= 94.64
= 95 m.
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 450 and 300 respectively. Find the distance between the two ships.

A is the aeroplane, D and C are the ships sailing towords A.
Ships are sailing towords the aeroplane in the same direction.
in the figure, height Ab = 1500 m.
To find: Distance between the ships, that is CD.
Solution:
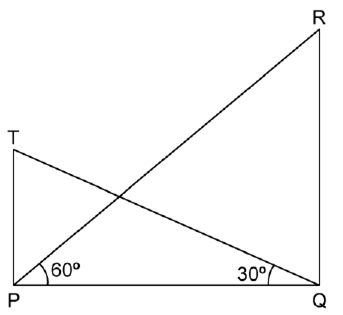
The angle of elevation from a point P of the top of a tower QR, 50 m high is 600 and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre.