Use graph paper to answer the following questions. (Take 2 cm = 1 unit on both axes)
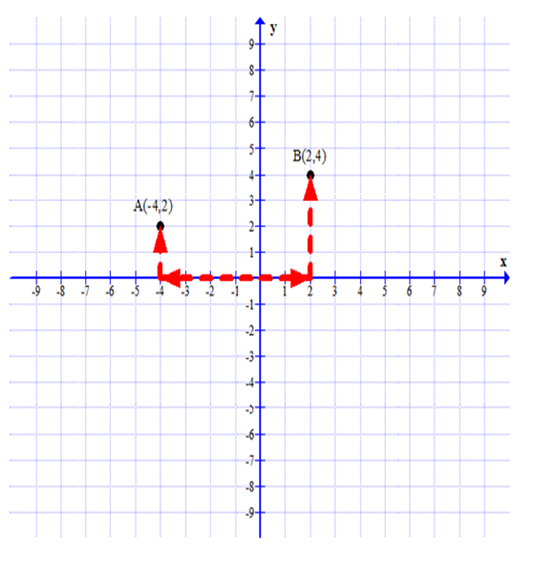
(i) Plot the points A( - 4, 2) and B(2, 4)
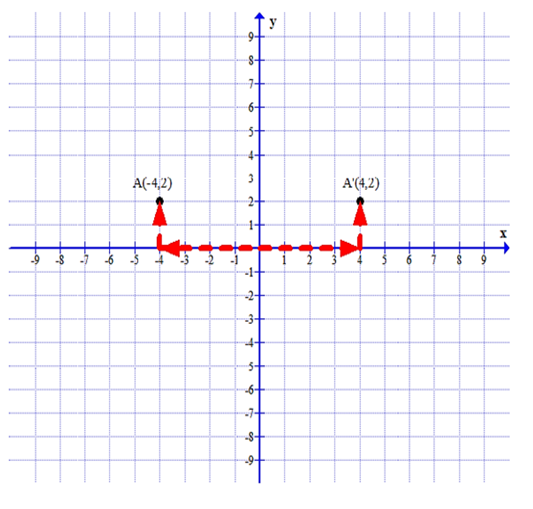
(ii) A' is the image of A when reflected at the y-axis. Plot it on the graph paper and write
the co-ordinates of A'.
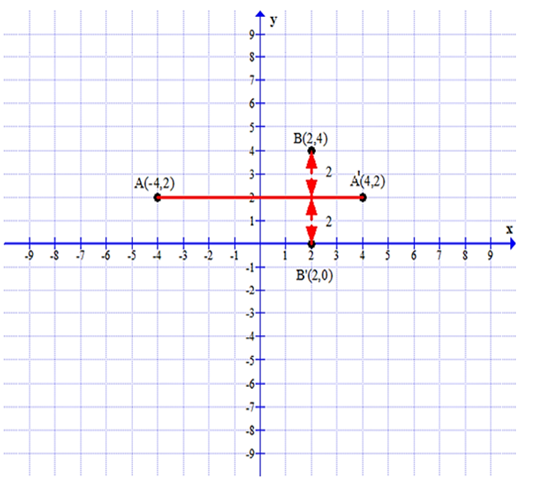
(iii) B' is the image of B when reflected on the line AA'. Write the co-ordinates of B'.
(iv) Write the geometric name of the figure ABA'B'.
(v) Name a line of symmetry of the figure formed.
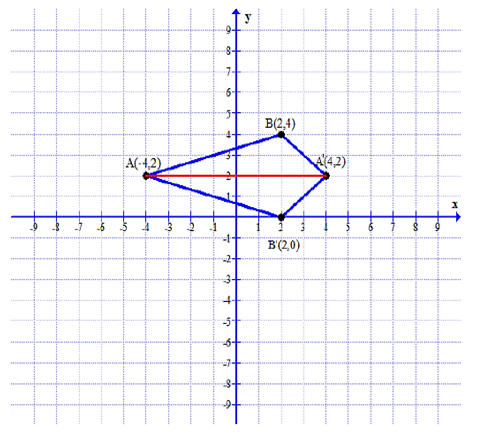
Consider 1 unit on the graph to be 2cm.
(i) Plotting points A(- 4, 2) and B(2, 4) on graph paper as follows.
(ii) The coordinates of A’ will be (4, 2).
(iii) The coordinates of B’ will be (2, 0).
(iv) The figure formed is kite shaped quadrilateral.
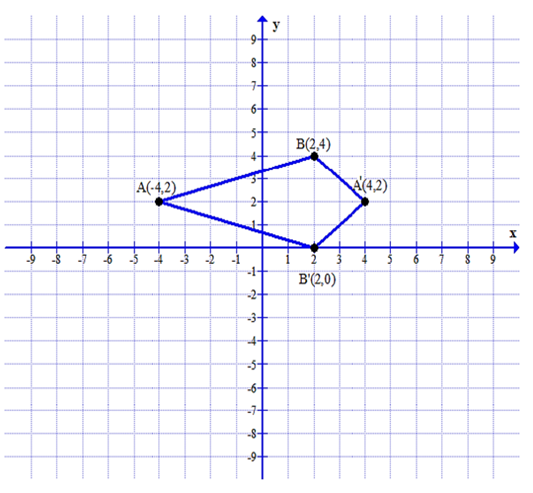
(v) A line of symmetry is a line which creates a mirror image on both sides. Thus, in the image, line AA’ is the line of symmetry.
(a) Use a graph paper for this question taking 1 cm = 1 unit along both the x and y axis :
(i) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
(ii) Reflect the points B, C, D and E on the y-axis and name them respectively as B’, C’, D’ and E’.
(iii) Write the coordinates of B’, C’, D’ and E’.
(iv) Name the figure formed by B C D E E’ D’ C’ B’.
(v) Name a line of symmetry for the figure formed.
Steps:
(i) See the figure.
(ii) Reflection of points on the y-axis will result in the change of the x-coordinate.
(iii) Points will be B’(−2, 5), C’(−5, 2), D’(−5, −2), E’(−2, −5).
(iv) The figure BCDEE’D’C’B’ is a hexagon.
(v) The lines of symmetry is x-axis or y-axis.

Use graph paper for this question. (Take 2 cm = 1 unit along both x and y axis.) Plot the points O ( 0, 0 ), A( - 4, 4 ), B ( - 3, 0 ) and C ( 0, - 3 )
(i) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates.
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure
( i)
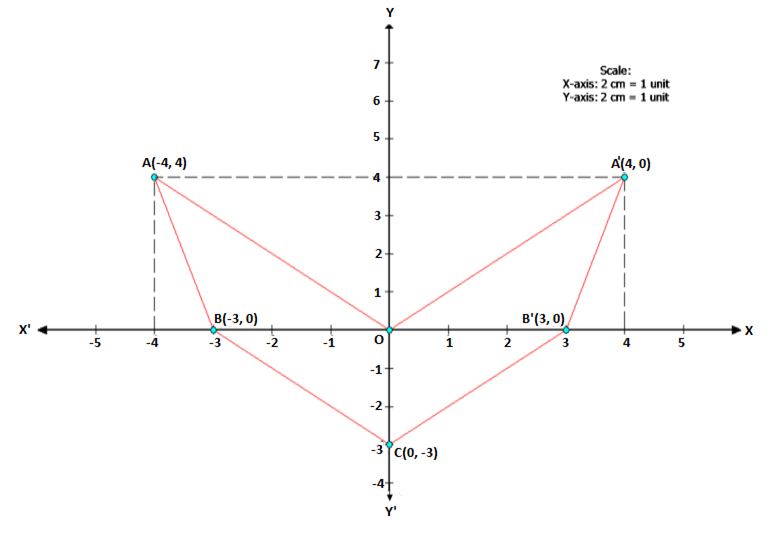
A' = ( 4, 4 ) and B' = ( 3, 0 )
( ii ) The figure is an arrow head.
( ii ) The y-axis is the line of symmetry of figure OABCB'A'.
Using a graph paper, plot the points A(6, 4) and B(0, 4).
(i) Reflect A and B in the origin to get the images A' and B'.
(ii) Write the co-ordinates of A' and B'.
(iii) State the geometrical name for the figure ABA' B'.
(iv) Find its perimeter.
(i) As given, we have to plot points A(6, 4) and B(0, 4) on graph paper.

(ii) Co-ordinates of A' = (–6, –4), Co-ordinates of B' = (0, –4)
(iii) ABA'B' is a parallelogram.
(iv) AB = A'B' = 6 units
In BA’B’,
BA' =
=
= 10 units
Thus, perimeter of ABA'B' = (6 + 10 + 6 + 10) units = 32 units.
Use graph paper for this question (Take 2 cm = 1 unit along both x and y axis). ABCD
is a quadrilateral whose vertices are A(2, 2), B(2, –2), C(0, –1) and D(0, 1).
(i) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD.
(ii) Write down the coordinates of A' and B'.
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A'B'CD.
( i ) and ( ii )

( iii ) D and C are invariant points.
( iv ) A'B'CD is a trapezium.
