We know that, Product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

(i) As chord CD and tangent at point T intersect each other at P,

PC  PD = PT²       ...(i)

AB is the diameter and tangent at point T intersect each other at P,

PA × PB = PT²       .(ii)

From (i) and (ii), PC × PD = PA × PB  …(iii)

Given: PD = 5cm, CD = 7.8cm

PA = PB + AB

    = 4 + AB

And, PC = PD + CD

            = 12.8cm

By substituting these values in equation (iii),

12.8 $\times$ 5 = (4 + AB) $\times$ 4

$\Rightarrow 4 + \mathrm{AB} = \frac{12.8 \times 5}{4}$

$\Rightarrow 4 + \mathrm{AB} = 16$

$\Rightarrow \mathrm{AB} = 12\mathrm{cm}$

(ii) PC $\times$ PD = PT²

^{$\Rightarrow \mathrm{PT} = 12.8 \times 5$}

^{$\Rightarrow$ PT = 8cm}

^{Therefore, the length of tangent is 8cm.}

Considering the given figure,

Given dimensions of the rectangle: AB = 14 cm and BC = 7 cm

Therefore, radius of quarter circle = $\frac{1}{2}{\mathrm{\pi r}}^2$

                                                 = $\frac{1}{4} \times \frac{22}{7} \times (7{)}^2$

                                                 = $\frac{77}{2}$sq.cm

Now, area of rectangle ABCD = AB $\times$ BC = 14 $\times$ 7 = 98 sq. cm
Required area = Area of rectangle ABCD - [Area of (BCEF) - Area of (DGE)]
                    = $98 - \frac{77}{2} - \frac{77}{4}$

                   = $\frac{161}{4}$

                   = 40.25 sq. cm

Construction : As given, we have to join AD and CB

In$∆$APD and $∆$CPB

We can write,

$\angle \mathrm{A} = \angle \mathrm{C}$       ($\because$ Angles are in same segment)

$\angle \mathrm{D} = \angle \mathrm{B}$       ($\because$ Angles are in same segment)

By AA Postulate,

$∆\mathrm{APD} ~ ∆\mathrm{CPB}$

$\Rightarrow \frac{\mathrm{AP}}{\mathrm{CP}} = \frac{\mathrm{PD}}{\mathrm{PB}}$ ($\because$ Corrosponding sides of similar triangles)

$\Rightarrow \mathrm{AP} \times \mathrm{PB} = \mathrm{CP} \times \mathrm{PD}$

Hence proved.

$$\begin{gathered} ( \mathrm{i} ) \angle \mathrm{BAQ} = 30° \\ \mathrm{Since} \mathrm{AB} \mathrm{is} \mathrm{the} \mathrm{bisector} \mathrm{of} \angle \mathrm{CAQ} \\ \Rightarrow \angle \mathrm{CAB} = \angle \mathrm{BAQ} = 30° \\ \mathrm{AD} \mathrm{is} \mathrm{the} \mathrm{bisector} \mathrm{of} \angle \mathrm{CAP} \mathrm{and} \mathrm{P} - \mathrm{A} - \mathrm{Q}, \\ \angle \mathrm{DAP} + \angle \mathrm{CAD} + \angle \mathrm{CAQ} = 180° \\ \Rightarrow \angle \mathrm{CAD} + \angle \mathrm{CAD} + 60° = 180° \\ \Rightarrow \angle \mathrm{CAD} = 60° \\ \mathrm{So}, \angle \mathrm{CAD} + \angle \mathrm{CAB} = 60° + 30° = 90° \\ \mathrm{Since} \mathrm{angle} \mathrm{in} \mathrm{a} \mathrm{semi}-\mathrm{circle} = 90° \\ \Rightarrow \mathrm{Angle} \mathrm{made} \mathrm{by} \mathrm{diameter} \mathrm{to} \mathrm{any} \mathrm{point} \mathrm{on} \mathrm{the} \mathrm{circle} \mathrm{is} 90° \end{gathered}$$

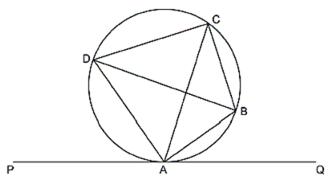
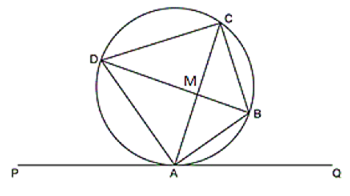
S0,  BD  is the diameter of the circle.

( ii )  Since  BD  is the diameter of the circle, so it will pass through the centre.

By  Alternate segment theorem,

$$\begin{gathered} \angle \mathrm{ABD} = \angle \mathrm{DAP} = 60° \\ \mathrm{So}, \mathrm{in} ∆\mathrm{BMA}, \\ \angle \mathrm{AMB} = 90° ........\left( \mathrm{Use} \mathrm{Angle} \mathrm{Sum} \mathrm{Property} \right) \end{gathered}$$

We know that perpendicular drawn from the centre to a chord of a circle bisects the chord.

$$\begin{gathered} \Rightarrow \angle \mathrm{BMA} = \angle \mathrm{BMC} = 90° \\ \mathrm{In} ∆\mathrm{BMA} \mathrm{and} ∆\mathrm{BMC}, \\ \angle \mathrm{BMA} = \angle \mathrm{BMC} = 90° \\ \mathrm{BM} = \mathrm{BM} ........( \mathrm{Common} \mathrm{side} ) \\ \mathrm{AM} = \mathrm{CM} .........( \mathrm{perpendicular} \mathrm{drawn} \mathrm{from} \mathrm{the} \mathrm{centre} \mathrm{to} \mathrm{a} \mathrm{chord} \mathrm{of} \mathrm{a} \mathrm{circle} \mathrm{bisects} \mathrm{the} \mathrm{chord}. ) \\ \Rightarrow ∆\mathrm{BMA} \cong ∆\mathrm{BMC} \\ \Rightarrow \mathrm{AB} = \mathrm{BC} ........( \mathrm{SAS} \mathrm{congruence} \mathrm{criterion} ) \\ \Rightarrow ∆\mathrm{ABC} \mathrm{is} \mathrm{an} \mathrm{isosceles} \mathrm{triangle}. \end{gathered}$$

In the given figure,

TS $\perp$ SP,

$\mathrm{m}\angle \mathrm{TSR} = \mathrm{m}\angle \mathrm{OSP} = {90}^{°}$

In $∆\mathrm{TSR}, \mathrm{m}\angle \mathrm{TSR} +\mathrm{m}\angle \mathrm{TSR} + \mathrm{m}\angle \mathrm{RTS} = {180}^{°}$

$\Rightarrow {90}^{°} + {65}^{°} + \mathrm{x} = {180}^{°}$

$\Rightarrow \mathrm{x} = {180}^{°} - {90}^{°} - {65}^{°}$

$\Rightarrow \mathrm{x} = {25}^{°}$

Now, y = 2x [Angle subtended at the centre is double that of angle subtended by the arc at the same centre]

$\Rightarrow \mathrm{y} = 2 \times {25}^{°}$

Therefore, $\mathrm{y} = {50}^{°}$

In $∆\mathrm{OSP}, \mathrm{m}\angle \mathrm{OSP} + \mathrm{m}\angle \mathrm{SPO} + \mathrm{m}\angle \mathrm{POS}= {180}^{°}$

$\Rightarrow \mathrm{z} = {180}^{° }- {140}^{°}$

Therefore, z = ${40}^{°}$