Let PQRS be the rectangle inscribed in the semi-circle of radius so that OR = r, where O is in centre of circle.

Let PO = OQ = x and QR = y so that sides of rectangle are of lengths 2x and 2y respectively.

Let $\angle \mathrm{QOR} = \mathrm{\theta }°$

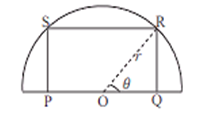
In $∆\mathrm{OQR}$,

$\frac{\mathrm{x}}{\mathrm{r}} = \cos \left(\mathrm{\theta }\right) \Rightarrow \mathrm{x} = \mathrm{rcos}\left(\mathrm{\theta }\right)$

$\frac{\mathrm{y}}{\mathrm{r}} = \sin \left(\mathrm{\theta }\right) \Rightarrow \mathrm{y} = \mathrm{rsin}\left(\mathrm{\theta }\right)$

Let A be area of rectangle PQRS

$\therefore \mathrm{A} = \mathrm{PQ} \times \mathrm{QR}$

       = 2 OQ $\times$ QR

       = ${\mathrm{r}}^2\sin \left(2\mathrm{\theta }\right)$

$\frac{d\mathrm{A}}{d\mathrm{\theta }} = 2{\mathrm{r}}^2\cos \left(\mathrm{\theta }\right)$ = 0

$\therefore 2\mathrm{\theta } = \frac{\mathrm{\pi }}{2}$ 

$\therefore \mathrm{\theta } = \frac{\mathrm{\pi }}{4}$ is critical point.

$\frac{d^2\mathrm{A}}{d{\mathrm{\theta }}^2} = - 4{\mathrm{r}}^2\sin \left(2\mathrm{\theta }\right)$

$\left(\frac{d^2\mathrm{A}}{d{\mathrm{\theta }}^2}\right){ }_{\mathrm{\theta } = \frac{\mathrm{\pi }}{4}} = - 4{\mathrm{r}}^2$ < 0

$\Rightarrow$ Area is maximum at $\mathrm{\theta }$ = $\frac{\mathrm{\pi }}{4}$

So, sides of rectangle are $\sqrt{2}\mathrm{r}, \frac{\sqrt{2}\mathrm{r}}{2}$

And, Area = $\sqrt{2}\mathrm{r} \times \frac{\sqrt{2}\mathrm{r}}{2}$ = r² sq. units.

Given, Face value of bill = Rs. 7650 = A

Discounted value of the bill = Rs. 7497

Bankers discount = Rs. (7650 - 7497) = Rs. 153

Tenure = 7 Months

$\therefore$ Nominal due date is 8^th october.

Legally due date = Nominal due date + 3 days of grace

                        = 11^th october

Number of unexpired days

Thus, number of unexpired days from 8 May to 11 October is 146 days.

n = $\frac{146}{365}$ = $\frac{2}{5}$ years.

Bankers discount = A x n x i

                    153 = 7650 x i $\times \frac{2}{5}$

                   $\therefore \mathrm{i} = \frac{1}{20} = 0.05$

                   $\therefore \mathrm{r} = 5 \%$

Hence, the required rate of interest is 5 % per annum.

(i) Total revenue function = x(100 - x)

Profit function = Revenue function - Cost function

                     = 100x - x² - (x³/3 - 7x² + 111x + 50)

                     = - x³/3 + 6x² - 11x - 50

dP/dx = - x² + 12x - 11

For maximum or minimum dP/dx = 0

x² + 12x + 11 = 0

x = 1, 11

d²P/dx² = - 2x + 12

            = - 2 $\times$ 11 + 12

            = - 10 < 0

Profit  is maximum when x = 11

(i) Given,  x = $\frac{24 - \mathrm{p}}{3}$

Total revenue function = px

Revenue function = $\frac{\mathrm{p}(24 - 2\mathrm{p})}{3}$

                       R = $\frac{24\mathrm{p} - 2{\mathrm{p}}^2}{3}$

$\frac{\mathrm{dR}}{\mathrm{dp}} = \frac{24 - 4\mathrm{p}}{3}$

For maximum or minimum dR/dp = 0

$\text{∴ (24 - 4p)/3 = 0}$

$\therefore \mathrm{p} = 6$

(ii) $\frac{d^2\mathrm{R}}{d{\mathrm{p}}^2} = \frac{- 4}{3}$

As - 4/3 < 0, R is maximum

Number of units x = $\frac{24 - 12}{3} = \frac{12}{3} = 4$

$\therefore \mathrm{x} = 4$

Hence, R is maximum when 4 units are demanded at the price of 6 per unit.

Let x be the number of units produced and sold.

Price per unit = Rs. 8

Revenue function = R(x) = 8x

Variable cost of the x units = 25 % of 8x

                                        = Rs. 2x

Total cost = c(x) = fixed cost + variable cost

Total cost = c(x) = 24000 + 2x

At break even point: R(x) = c(x)

$\text{∴ 8x = 24000 + 2x}$

$\therefore \mathrm{x} = 4000$