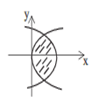
y² = 4 - 3x    ...(i)

y² = x         ...(ii)

Solving equation (i) and (ii), we get

4x = 4, x = 1

Required Area = 

                      = 2${\left[\frac{{\left(\mathrm{x}\right)}^{3/2}}{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right]}_0^1 +\hspace{0.17em}{\left[\frac{{\left(4 - 3\mathrm{x}\right)}^{3/2}}{3/2} \frac{1}{3}\right]}_1^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$

                     =  $2\left[\frac{1}{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right] + \left[\frac{{\left(4 - 3 \times {\displaystyle \frac{4}{3}}\right)}^{3/2}}{3/2} - \frac{{\left(4 - 3\right)}^{3/2}}{3/2}\right]\frac{1}{3}$

                     = $2\left[\frac{2}{3}\right] + \left[\frac{2}{3} \times \frac{1}{3}\right]$

                     = $2\left(2/3 + 2/9\right)$

                     = 16/9 sq. units.

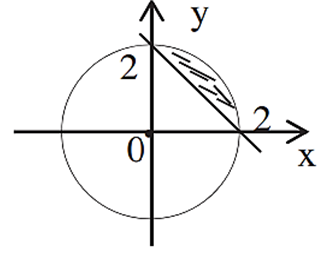
The required area = ${\int }_0^2\sqrt{4 - {\mathrm{x}}^2}d\mathrm{x} - {\int }_0^2\left(2 - \mathrm{x}\right)d\mathrm{x}$

                           = ${\left[\frac{\mathrm{x}}{2}\sqrt{4 - {\mathrm{x}}^2} + \frac{{\displaystyle 4}}{2}{\sin }^{-1}\left(\frac{\mathrm{x}}{2}\right)\right]}_0^2 - {\left[2\mathrm{x} - \frac{{\mathrm{x}}^2}{2}\right]}_0^2$

                           = $\left[1 \times \sqrt{0} + 2 {\sin }^{-1}\left(1\right) - 0\sqrt{4} - 2 \times 0 - \left[2 \times 2 - \frac{4}{2} - 2 \times 0 + \frac{0}{2}\right]\right]$

                           = $2{\sin }^{-1}\left(1\right) + 4 - 2 - 0 + 0$

                           = $2 \times \frac{\mathrm{\pi }}{2} - 2$

                           = $\mathrm{\pi } - 2$ sq. units.

Solving, x = y, y = 2x - x²,

2x - x² = x

x² - x = 0

$\mathrm{x}(\mathrm{x} - 1) = 0$

x = 0, 1

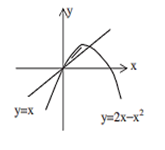
Required Area = ${\int }_0^1\left({\mathrm{y}}_{1 }- {\mathrm{y}}_2\right)d\mathrm{x}$

                     = ${\int }_0^1\left\{\left(2\mathrm{x} - {\mathrm{x}}^2\right) - {\mathrm{x}}^2\right\}d\mathrm{x}$

                     = ${\int }_0^1\left(\mathrm{x} - {\mathrm{x}}^2\right)d\mathrm{x}$

                    = ${\left[\frac{{\mathrm{x}}^2}{2} - \frac{{\mathrm{x}}^3}{3}\right]}_0^1$

                    = $\left(\frac{1}{2} - \frac{1}{3}\right) - \left(0\right) = \frac{1}{6}$ sq. units

The curve y = 6x - x²

Therefore, y = -(x - 3)² + 9 

y = -(x - 3)² + 9 represents parabola with vertex at (3, 9) and it opens downward.

The curve y = x² - 2x = (x - 1)² - 1

y = (x - 1)² - 1 represents a parabola with vertex at (1, - 1) and it opens upward.

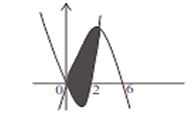
Both the curves pass through origin and intersect in the first quadrant at (4, 8)

Required area = ${\int }_0^4(6\mathrm{x} - {\mathrm{x}}^2)d\mathrm{x} - {\int }_0^4({\mathrm{x}}^2 - 2\mathrm{x})d\mathrm{x}$

                     = ${\int }_0^4(8\mathrm{x} - 2{\mathrm{x}}^2).d\mathrm{x}$

                    = ${\left[8.\frac{{\mathrm{x}}^2}{2} - 2.\frac{{\mathrm{x}}^3}{3}\right]}_0^4$

                    = $64 - \frac{128}{3}$

                    = $\frac{64}{3}$ sq. units