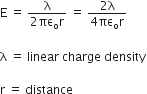
E = 9 x io4 N/C
r = 2 cm = 2 x 10-2 m
Hence,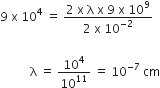 
Gauss’s theorem : It states that the electric flux fE, through any closed surface is 1/Î0 times the total charge q enclosed by the surface.
Mathematically, 
A short electric dipole (consists of two point charges +q and -q) is placed at the centre O and inside a large cube (ABCDEFGH) of length L, as shown in the figure below. The electric flux, remaining through the cube is:
Zero
B.
Zero
Since, it is an electric dipole, the net charge enclosed by the surface is zero. Therefore, according to Gauss's law, electric flux through the cube will be zero.
a) Two point charges Q1 = 400 
and Q2 = 100 
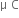are kept fixed, 60 cm apart in vacuum.Find intensity of the electric field at midpoint of the line joining Q1 and Q2.
b) i) State Gauss' law.
ii) In an electric dipole, at which point is the electrical potential zero?
a) Given:
Q1 = 400 
= 400 x 10-6 C
Q2 = 100 
= 100 x 10-6 C
x = 60 cm = 60 x 10-2 m
Electric field intensity at mid-point P by charge Q1 is given by,
E1 =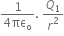 
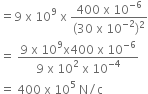
Electric field intensity at mid point P by charge Q2 is given by,
E2 =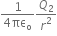 
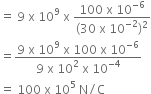
Total electric field intensity at mid point P is given by,
E = E1 - E2
= 400 x 105 - 100 x 105
= 300 x 105 N/C
Direction of electric field intensity at mid point P is from Q1 to Q2.
b) i) Gauss Theorem states that the electric flux 
through any closed surface is equal to 
times the net charge q enclosed by the surface.
Mathematically,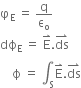
ii) At the mid point of an electric dipole electric potential is zero.
Switch
