Construction: Take a point P on AC such that BP bisects ∠B. Join P and D.
Proof: In ∆ABC,
∵ BP bisects ∠ABC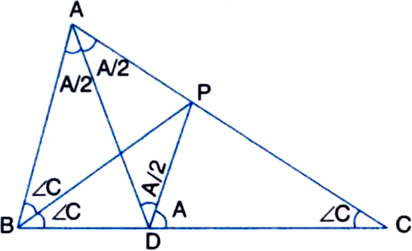




In APBC,
∴ ∠PBC = ∠PCB (= ∠C)
∴ PB = PC    ...(2)
| Sides opposite to equal angles of∆PBC In ∆APB and ∆DPC,
AB = CD    | Given
PB = PC    | From (2)
∠ABP = ∠DCP (= ∠C)
∴ ∆APB ≅ ∆DPC    | SAS Axiom
∴ ∠BAP = ∠CDP (= ∠A)    ...(3)
| C.P.C.T.
and    AP = DP    ...(4) | C.P.C.T.
In ∆APD,
∵ AP = DP    | From (4)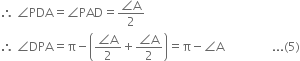

Again from ∆DPC,
∠DPC = π - (∠A + ∠C)
∴ ∠DPA = π - ∠DPC = π - {π - (∠A + ∠C)} = ∠A + ∠C    ...(6)
From (5) and (6),
π - A = ∠A + ∠C ⇒ 2∠A + ∠C = π ...(7)
Again,
∠A + ∠B + ∠C = π
| ∵ The sum of three angles of ∆ABC = π ⇒ ∠A + 2∠C + ∠C = π | ∵ ∠B = 2∠C
⇒    ∠A + 3∠C = π    ...(8)
Multiplying (7) by 3, we get
6∠A + 3∠C = 3π    ...(9)
Subtracting (8) from (9), we get

         

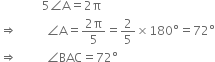
A.

D.

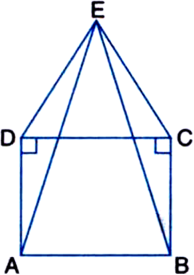
Given: ABCD is a square and ∆DEC is an equilateral triangle.

To Prove:

(i)    ∆ADE ≅ ∆BCE

(ii)    AE = BE

(iii)    ∠DAE = 15°

Proof: (i) In ∆ADE and ∆BCE,
   AD = BC

           

  DE=CE
    
          

 

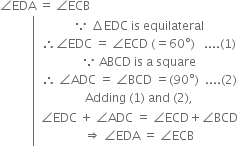
∴ ∆ADE ≅ ∆BCE | SAS congruence rule
(ii)    ∵ ∆ADE ≅ ∆BCE | Proved in (1)
∴ AE = BE    | CPCT
(iii)    In ∆DAE,
∵ DE = DA    | Given
∴ ∠DAE = ∠DEA    ...(1)
| Angles opposite to equal sides of a triangle are equal Also, ∠ADE + ∠DAE + ∠DEA = 180°
| Angle sum property of a triangle
⇒ (∠ADC + ∠EDC) + ∠DAE + ∠DEA = 180°
⇒ (90° + 60°) + ∠DAE + ∠DEA = 180°
⇒ ∠DAE + ∠DEA = 30°    ...(2)
From (1) and (2),
∠DAE = 15° = ∠DEA

Given: ABC is an equilateral triangle whose medians are AD, BE and CF.
To Prove: AD = BE = CF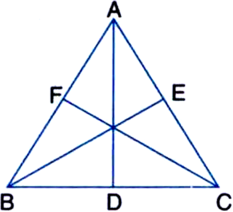



Proof: In ∆ADC and ∆BEC,

                AC = BC

                      

                

                     
           
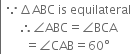
              DE = EC

                  


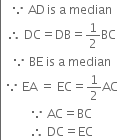
                         | SAS congruence rule

                         ....(1) | CPCT  

Similarly, we can prove that
BE = CF    ...(2)
and    CF = AD    ...(3)
From (1), (2) and (3)
AD = BE = CF