A class has 30 students. In how many ways can three prizes be awarded so that:
(a) no students get more than one prize?
(b) a student may get any number of prizes?
(a) Number of ways in which the first prize can be awarded = 30![]() m = 30
m = 30
Number of eligible students for the second prize = 29
∴ Number of ways in which second prize can be awarded = 29![]() n = 29
n = 29
Number of ways in which the third prize can be awarded = 28![]() P = 28
P = 28
∴ By fundamental principle of counting, the total number of ways of awarding the three prizes.
= ![]()
(b) Number of students = 30
Number of ways in which the first prize may be awarded = 30![]() m = 30
m = 30
Number of students eligible for the second prize = 30 (∵ A student may get any number of prizes)
Number of ways in which the second prize can be awarded = 30![]() n = 30
n = 30
Similarly, number of ways in which the third prize can be awarded = 30![]() p = 30
p = 30
By fundamental principle of counting, the number of ways in which the three prizes can be awarded
= ![]()
Total flags = 5
Number of signals generated, using two flags:
![]()
= m x n = 5 x 4 = 20 ...(i)
Or
Number of signals generated, using three flags:
![]()
= m x n x p = 5 x 4 x 3 = 60 ...(ii)
Or
Number of signals generated, using 4 flags:
![]()
= m x n x p x q = 5 x 4 x 3 x 2 = 120.
Or
Number of signals generated, using all 5 flags:
![]()
= m x n x p x q x r = 5 x 4 x 3 x 2 x 1 = 120
∴ Total number of signals generated
= 20 + 60 + 120 +120 = 320.
Solution not provided.
Ans. 12
Digits available are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Total number of digits = 10
Number of digits used = 3
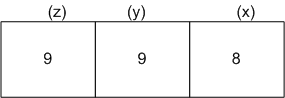
Number of filling box (z) = 9 [∴ If 0 is put in there, it becomes a two digit number]![]() m = 9
m = 9
Number of ways of filling box (y) = 9 (3 Repetition is not allowed)![]() n = 9
n = 9
Number of ways of filling box (x) = 8 (3 Repetition is not allowed)![]() p = 8
p = 8
∴ The number of 3 digit numbers or numbers between 100 and 1000
= m x n x p = 9 x 9 x 8 = 648
