A bag X contains 4 white balls and 2 black balls, while another bag Y contains 3 white balls and 3 black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag Y.
Given,
Bag X =4 white, 2 black
Bag Y=3 white, 3 black
Let A be the event of selecting one white and one black ball.
E1 = first bag selected
E2 = second bag selected
In a set of 10 coins, 2 coins are with heads on both the sides. A coin is selected at random from this set and tossed five times. If all the five times, the result was heads, find the probability that the selected coin had heads on both the sides
Let E1 E1 and A be the events defined as follows:
E1 = Selecting a coin having head on both the sides
E1= Selecting a coin not having head on both the sides
A = Getting all heads when a coin is tossed five times
We have to find P(E1/A).
There are 2 coins having heads on both the sides.
There are 8 coins not having heads on both the sides.
By Baye's Theorem, we have
Three numbers are selected at random (without replacement) from first six positive integers. Let X denote the largest of the three numbers obtained. Find the probability distribution of X.Also, find the mean and variance of the distribution.
The first six positive integers are 1, 2, 3, 4, 5, 6.
We can select the two positive numbers in 6 × 5 = 30 different ways.
Out of this, 2 numbers are selected at random and let X denote the larger of the two numbers.
Since X is large of the two numbers, X can assume the value of 2, 3, 4, 5 or 6.
P (X =2) = P (larger number is 2) = {(1,2) and (2,1)} = 2/1
P (X = 3) = P (larger number is 3) = {(1,3), (3,1), (2,3), (3,2)} =4/3
P (X = 4) = P (larger number is 4) = {(1,4), (4,1), (2,4), (4,2), (3,4), (4,3)} = 6/30
P (X = 5) = P (larger number is 5) = {(1,5), (51,), (2,5), (5,2), (3,5), (5,3), (4,5), (5.4)} = 8/30
P (X = 6) = P (larger number is 6) = {(1,6), (6,1), (2,6), (6,2), (3,6), (6,3), (4,6), (6,4), (5,6), (6,5)} = 10/30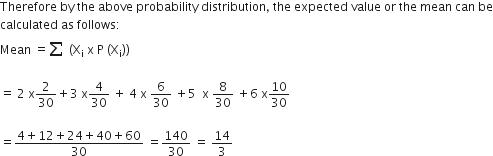
A and B throw a pair of dice alternately, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
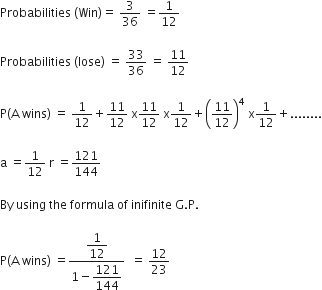
How many times must a fair coin be tossed so that the probability of getting at least one head is more than 80%?
Let p denotes the probability of getting heads.
Let q denotes the probability of getting tails.
Suppose the coin is tossed n times.
Let X denote the number of times of getting heads in n trails. 
So the fair coin should be tossed for 3 or more times for getting the required probability.
