
Given,
Length of loop, l = 8 cm = 8 x 10–2 m
Breadth of loop, b = 2 cm = 2 x 10–2 m
Strength of magnetic field, B = 0.3 T
Velocity of loop, v = 1 cm/sec = 10–2 m/sec
Let the field be perpendicular to the plane of the paper directed inwards.
(i)Then, the magnitude of induced emf is,
Time for which induced e.m.f. will last is equal to the time taken by the coil to move outside the field
(ii) The conductor is moving outside the field normal to the shorter side.
b = 2 x 10–2 m
∴ The magnitude of induced emf is
Time,
Use Lenz’s law to determine the direction of induced current in the situation described by Fig:
(a) A wire of irregular shape turning into a circular shape;
(b) A circular loop being deformed into a narrow straight wire.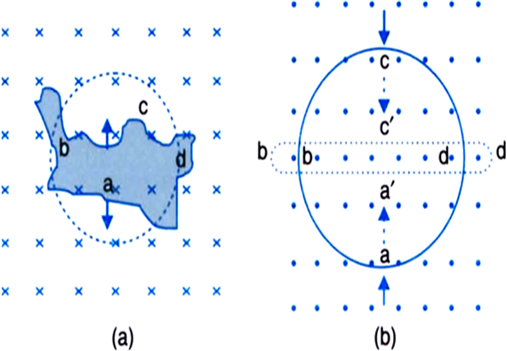
(a) When a wire of irregular shape turns into a circular loop, area of the loop tends to increase. Therefore, magnetic flux linked with the loop increases. According to Lenz’s law, the direction of induced current must oppose the change in magnetic field, for which induced current should flow along adcba (anticlockwise).
(b) In this case, the magnetic flux tends to decrease. Therefore, induced current must support the magnetic field, for which induced current should flow along adcba (anticlockwise).
Predict the direction of induced current in the situations described by the following figs.(a) to(f).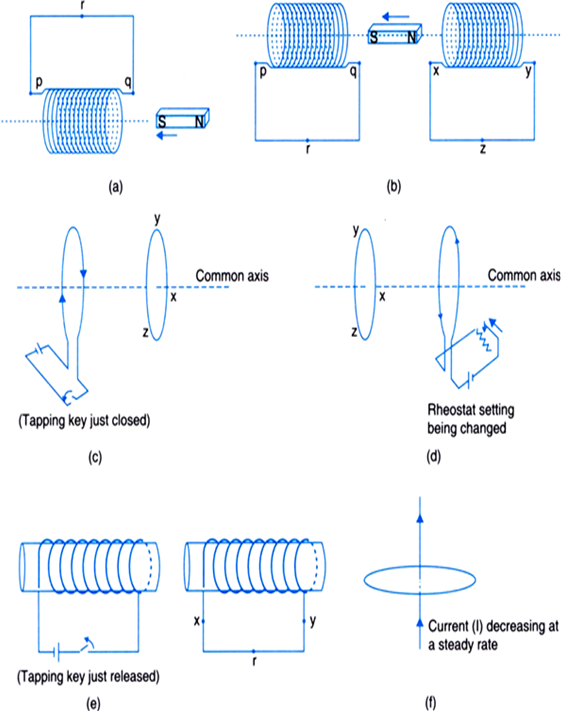
(a) South pole develops at end q and the induced current should flow clockwise. Therefore, induced current in the coil flows from qr to pq.
(b) Coil pq in this case would develop S-pole at q and coil XY would also develop S pole at X. Therefore, induced current in coil pq will be from q to p and induced current in the coil XY will be from Y to X.
(c) North pole is moving away from the coil hence, induced current in the right loop will be along XYZ.
(d) Induced current in the left loop will be along ZYX as seen from front.
(e) Induced current in the right coil is from X to Y.
(f) Since magnetic lines of force lie in the plane of the loop, no current is induced.
