Diameter of cylinder (d) = 2 m
Radius of cylinder (r) = 1 m
Height of cylinder (H) = 5 m
Volume of cylindrical tank, Vc = πr²H = π×(1)2×5=5π m

Length of the park (l) = 25 m
Breadth of park (b) = 20 m
the height of standing water in the park = h
Volume of water in the park = lbh = 25×20×h

Now water from the tank is used to irrigate the park. So,
Volume of cylindrical tank = Volume of water in the park

⇒5π=25×20×h
⇒5π/25×20=h
⇒h=π/100 m
⇒h=0.0314 m

Through recycling of water, better use of the natural resource occurs without wastage. It helps in reducing and preventing pollution.
It thus helps in conserving water. This keeps the greenery alive in urban areas like in parks gardens etc.

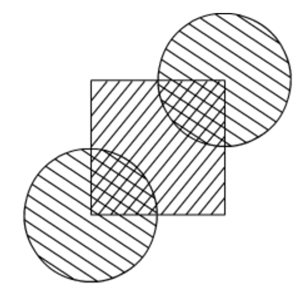
Side of square = 28 cm and radius of each circle = 28/2 cm
Area of the shaded region
= Area of the square + Area of the two circles − Area of the two quadrants

Let the height and radius of the given cone be H and R respectively.

The cone is divided into two parts by drawing a plane through the mid point of its axis and parallel to the base.

Upper part is a smaller cone and the bottom part is the frustum of the cone.
⇒ OC = CA = h/2

Let the radius of smaller cone be r cm.

In Δ OCD and Δ OAB,
∠OCD = ∠OAB = 90°
∠COD = ∠AOB (common)
∴ Δ OCD ∼ Δ OAB (AA similarity)

⇒ OA/OC = AB/CD = OB/OD
⇒ h / h/2 = R/r
⇒ R = 2r

The radius and height of the cone OCD are r cm and h/2 cm

Therefore the volume of the cone OCD = 1/3 x π x r² x h/2 = 1/6 πr²h

Volume of the cone OAD = 1/3 x π x R² x h = 1/3 x π x 4r² x h

The volume of the frustum = Volume of the cone OAD - Volume of the cone OCD
= (1/3 x π x 4r² x h) – (1/3 x π x r² x h/2)
= 7/6 πr²h

Ratio of the volume of the two parts = Volume of the cone OCD : volume of the frustum
= 1/6 πr²h : 7/6 πr²h
= 1 : 7

Height of the solid metal cylinder, h = 10 cm
Radius of the solid metal cylinder, r = 4.2 cm

therefore,

Radius of each hemisphere = radius of the solid metal cylinder, r = 4.2 cm

Now, 

Volume of the rest of the cylinder = Volume of cylinder - 2 x volume of each hemisphere

 

Thickness of the cylindrical wire = 1.4 cm
Therefore, 
Radius of the cylindrical wire, R = 1.4/2 = 0.7 cm

Let the length of the wire be H cm.

It is given that the rest of the cylinder is melted and converted into a cylindrical wire.

therefore,

Volume of the cylindrical wire = Volume of the rest of the cylinder

⇒ π x 0.7 x 0.7 x H = π x (4.2)² x (4.4)



Hence, the length of the wire is 158.4 cm

Area of the square lawn PQRS = 42 m x 42 m

Let OP = OS = xm
So, x² + x²  = (42)²

⇒ 2x² = 42 x 42

⇒ x² = 21 x 42

Now,
area of sector POS=