---

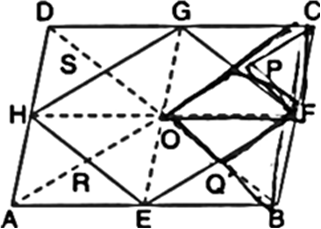
Given: E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD.



To Prove: ar(EFGH) = 

ar(ABCD).
Construction: Join OF, OG, OH and OE. Also, join AC and BD.
Proof: In ΔBCD,
∵    F and G are the mid-points of BC and DC respectively.
∴ FG || BD    ...(1)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
In ΔBAD,
∵ E and H are the mid-points of AB and AD respectively.
EH || BD    ...(2)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
From (1) and (2),
EH || FG    ...(3)
Similarly, we can prove that
EF || HG    ...(4)
From (3) and (4),
Quadrilateral EFGH is a parallelogram
| A quadrilateral is a parallelogram if its opposite sides are equal
∵    F is the mid-point of CB and O is the mid-point of CA
FO || BA
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side and is half of it ⇒    FO || CG    ...(5)
V BA || CD (opposite sides of a parallelogram are parallel)
∴ BA || CG

and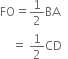    

∵ Opposite sides of a parallelogram are equal = CG    ...(6)
| ∵ G is the mid-point of CD In view of (5) and (6),
Quadrilateral OFCG is a parallelogram
∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of
equal length
∵ OP = PC
| ∵ Diagonals of a || gm bisect each other
∵ ΔOPF and ∵CPF have equal bases
(∵ OP = PC) and have a common vertex F Their altitudes are also the same ar(ΔOPF) = ar(ΔCPF)
Similarly, ar(ΔOQF) = ar(ΔBQF)
Adding, we get
ar(ΔOPF) + ar(ΔOQF) = ar(ΔCPF) + ar(ΔBQF) ⇒ ar(|| gm OQFP) = ar(ΔCPF) + ar(ΔBQF)                                                               ....(7)
Similarly,
ar(|| gm OPGS) = ar(⇒GPC) + ar(⇒DSG)                 ...(8)
ar(|| gm OSHR) = ar(ΔDSH) + ar(ΔHAR)
ar(|| gm OREQ) = ar(ΔARE) + ar(ΔEQB)                 ...(10)
Adding the corresponding sides of (7), (8), (9) and (10), we get
ar(|| gm EFGH) = {ar(ACPF} + ar(ΔGPC)}
+ {ar(ΔDSG) + ar(ΔDSH)} + {ar(ΔHAR) + ar(ΔARE)} + (ar(ΔBQF) + ar(ΔEQB)}
= ar(ΔFCG) + ar(ΔGDH) + ar(ΔHAE) + ar(ΔEBF)

---

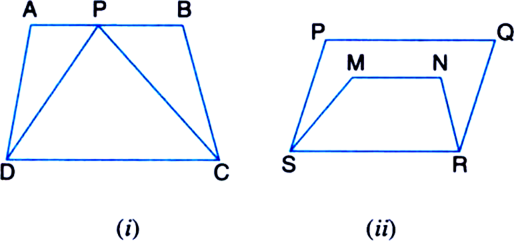
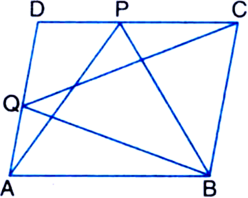
(i) ΔPDC and quadrilateral ABCD lie on the same base DC and between the same parallels DC and AB.

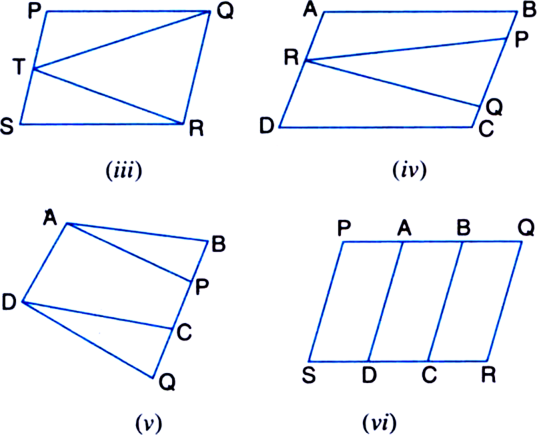
(iii) ΔTRQ and parallelogram SRQP lie on the same base RQ and between the same parallels RQ and SP.

(v) Quadrilaterals APCD and ABQD lie on the same base AD and between the same parallels AD and BQ.

---

Given: P is a point in the interior of a parallelogram ABCD.

To Prove : (i) 
ar(|| gm ABCD)
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
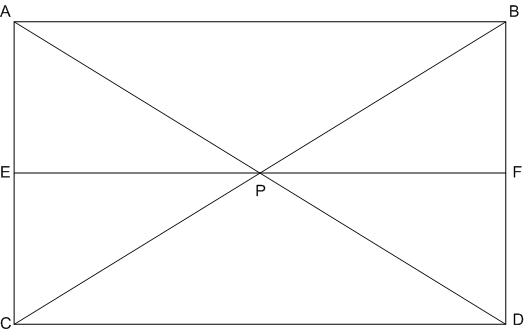
Construction: Through P, draw a line EF parallel to AB.



Proof: (i) EF || AB ...(1) | by construction
∵ AD || BC
∵ Opposite sides of a parallelogram are parallel
∴ AE || BF    ...(2)
In view of (1) and (2),
Quadrilateral ABFE is a parallelogram
A quadrilateral is a parallelogram if its opposite sides are parallel
Similarly, quadrilateral CDEF is a parallelogram
∵ ΔAPB and || gm ABFE are on the same base AB and between the same parallels AB and EF.


∵ ΔPCD and || gm CDEF are on the same base DC and between the same parallels DC and EF.


Adding (3) and (4), we get ar(ΔAPB) + ar(ΔPCD)

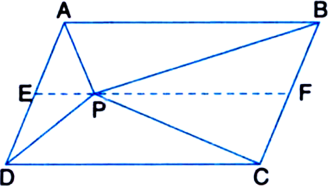
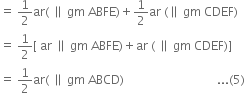
(ii) ar(ΔAPD) + ar(ΔPBC)
= ar(|| gm ABCD) – [ar(ΔAPB) + ar(ΔPCD)] = 2 [ar(ΔAPB) + ar(ΔPCB)] – [ar(ΔAPB) + ar(ΔPCD)]
= ar(ΔAPB) + ar(ΔPCD).

---

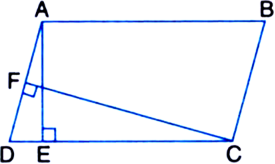
ar(parallelogram ABCD) = AB x AE = 16 x 8 cm²
= 128 cm²    ...(1)
ar(parallelogram ABCD) = AD x CF
= AD x 10 cm²    ...(2)
From (1) and (2), we get

AD X 10 = 128


  ad = 12.8 cm

---

Given: P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD.



To Prove: ar(ΔAPB) = ar(ΔBQC).
Proof: ∵ ΔAPB and || gm ABCD are on the same base AB and between the same parallels AB and DC.


∵ ΔBQC and || gm ABCD are on the same base BC and between the same parallels BC and AD.


From (1) and (2),
ar(ΔAPB) = ar(ΔBQC).