
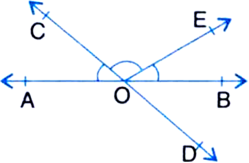
∵ Lines AB and CD intersect at O
∴ ∠AOC = ∠BOD
| Vertically Opposite Angles
But ∠BOD = 40° ...(1) | Given
∴ ∠AOC = 40° ...(2)
Now, ∠AOC + ∠BOE = 70°
⇒ 40° + ∠BOE = 70° | Using (2)
⇒ ∠BOE = 70° - 40°
⇒ ∠BOE = 30°
Again,
Reflex ∠COE
= ∠COD + ∠BOD + ∠BOE
= ∠COD + 40° + 30°
| Using (1) and (2)
= 180° + 40° + 30°
| ∵ Ray OA stands on line CD
|∴ ∠AOC + ∠AOD = 180° (Linear Pair Axiom) ⇒ ∠COD = 180°
= 250°.
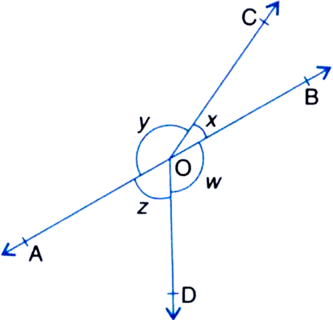
x + y = w + z ...(1) | Given
∵ The sum of all the angles round a point is equal to 360°.![]() x + y + w + z = 3600
x + y + w + z = 3600 ![]() x + y + x + y = 3600 | Using (1)
x + y + x + y = 3600 | Using (1)![]() 2(x + y) = 3600
2(x + y) = 3600![]()
![]() x + y = 1800
x + y = 1800
∴ AOB is a line.
| If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
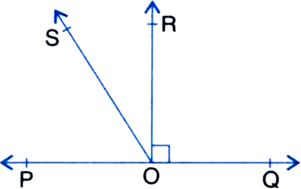
∵ Ray OR is perpendicular to line PQ.
∴ ∠QOR = ∠POR = 90° ...(1)
∠QOS = ∠QOR + ∠ROS ...(2)
∠POS = ∠POR - ∠ROS ...(3)
From (2) and (3),
∴ ∠QOS - ∠POS = (∠QOR - ∠POR) + 2∠ROS = 2∠ROS | Using (1)![]()
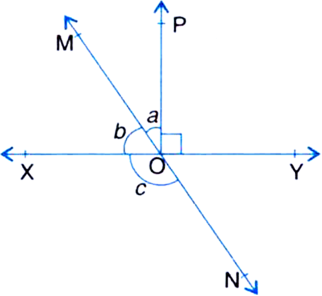
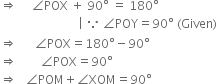
∵ Ray OX stands on line MN
∴ ∠XOM + ∠XON = 180°
| Linear Pair Axiom
⇒ b + c = 180°
⇒ 54° + c = 180° | Using (2)
⇒ c = 180° - 54°
⇒ c = 126°.
