


 πr3N
πr3N  × 3.14 × (1.5 × 108)3 × 6.023 × 1023
× 3.14 × (1.5 × 108)3 × 6.023 × 1023 
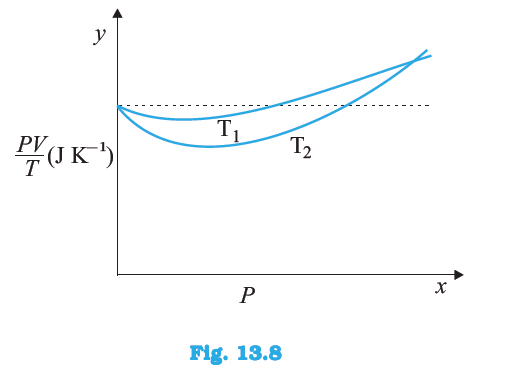
 at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of
at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of  (for low-pressure high-temperature region of the plot)?
(for low-pressure high-temperature region of the plot)?  is equal.
is equal.  , where the two curves meet, is μR. This is because the ideal gas equation is given as,
, where the two curves meet, is μR. This is because the ideal gas equation is given as,  = μR
= μR  =
=  × 8.314
× 8.314  , where the curves meet on the y-axis, is
, where the curves meet on the y-axis, is at the point where the curves meet the y-axis.
at the point where the curves meet the y-axis.  = 0.26 J K-1
= 0.26 J K-1 = μR, at constant temperature
= μR, at constant temperature ×
× 
 .
.



