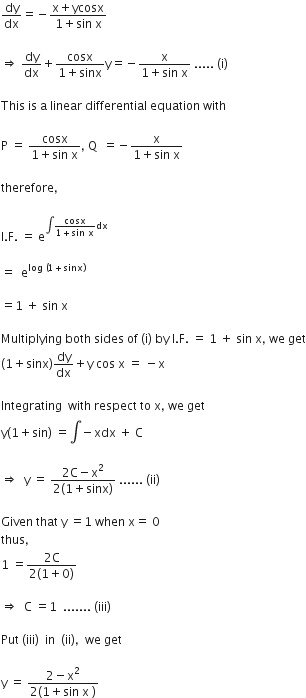Find the particular solution of the differential equation from
    • Zigya Logo

    Differential Equations
    pdf download
    If space straight x to the power of straight x plus straight x to the power of straight y plus straight y to the power of straight x space equals space straight a to the power of straight b comma space space then space find space dy over dx.
    straight x to the power of straight x plus straight x to the power of straight y plus straight y to the power of straight x space equals straight a to the power of straight b space space space... left parenthesis straight i right parenthesis Let space straight u space equals space straight x to the power of straight x log space straight u space equals space straight x space log space straight x 1 over straight u. du over dx equals straight x.1 over straight x plus log space straight x therefore space space du over dx equals straight x to the power of straight x left parenthesis 1 plus log space straight x right parenthesis Let space straight v equals space straight x to the power of straight y log space straight v space equals space straight y space log space straight x 1 over straight v. dv over dx space equals space open parentheses straight y over straight x plus log space straight x dy over dx close parentheses therefore space dv over dx equals straight x to the power of straight y open parentheses straight y over straight x plus logx dy over dx close parentheses Let space straight w space equals straight y to the power of straight x Log space straight w space equals space straight x space log space straight y 1 over straight w. dw over dx equals space open parentheses straight x over straight y. dy over dx plus log space straight y close parentheses therefore space dw over dx equals straight y to the power of straight x open parentheses log space straight y space plus space straight x over straight y. dy over dx close parentheses

    left parenthesis straight i right parenthesis space can space be space writeen space as straight u plus straight v plus straight w space equals space straight a to the power of straight b du over dx plus dv over dx plus dw over dx equals 0 rightwards double arrow space space straight x to the power of straight x left parenthesis 1 plus logx right parenthesis plus straight x to the power of straight y open parentheses straight y over straight x plus logx dy over dx close parentheses plus straight y to the power of straight x open parentheses logy plus straight x over straight y dy over dx close parentheses space equals space 0 rightwards double arrow space space straight x to the power of straight x plus straight x to the power of straight x logx plus straight x to the power of straight y. straight y over straight x plus straight x to the power of straight y. logx. dy over dx plus straight y to the power of straight x. logy plus straight y to the power of straight x. straight x over straight y. dy over dx equals 0 rightwards double arrow space space dy over dx open parentheses straight x to the power of straight y. logx space plus space straight y to the power of straight x. straight x over straight y close parentheses space equals space straight x to the power of straight x plus straight x to the power of straight x logx plus straight x to the power of straight y. straight y over straight x plus straight y to the power of straight x. log space straight y rightwards double arrow dy over dx open parentheses straight x to the power of straight y. logx space plus space xy to the power of straight x minus 1 end exponent close parentheses space equals space open parentheses straight x to the power of straight x plus straight x to the power of straight x logx plus yx to the power of straight y minus 1 end exponent plus straight y to the power of straight x. log space straight y close parentheses therefore space space dy over dx equals fraction numerator left parenthesis straight x to the power of straight x plus straight x to the power of straight x logx space plus yx to the power of straight y minus 1 end exponent plus straight y to the power of straight x. log space straight y right parenthesis over denominator left parenthesis straight x to the power of straight y. logx plus xy to the power of straight x minus 1 end exponent right parenthesis end fraction

    513 Views
    Answer

    Find the differential equation of the family of lines passing through the origin. 

    Consider the equation, y = mx, where m is the parameter.
    Thus, the above equation represents the family of lines which pass through the origin.
    y = mx    ....(1)
     rightwards double arrow space space straight y over straight x space equals space straight m space... left parenthesis 2 right parenthesis 
    Differentiating the above equation (1) which respect to x,
       straight y space equals space mx dy over dx space equals space straight m space cross times space 1 space space rightwards double arrow space space dy over dx equals straight m space space space rightwards double arrow space dy over dx space equals space straight y over straight x space left square bracket because space from space equation space left parenthesis 2 right parenthesis right square bracket space space space space rightwards double arrow dy over dx minus space straight y over straight x space equals space 0 space
    Thus we have eliminated the constant, m.
    The required differential equation is
    dy over dx minus straight y over straight x space equals 0

    1357 Views
    Answer
    If space straight y space equals space straight e to the power of ax. cosbx comma space then space prove space that space space space fraction numerator straight d squared straight y over denominator dx squared end fraction minus 2 straight a dy over dx plus left parenthesis straight a squared plus straight b squared right parenthesis straight y space equals space 0
    straight y equals straight e to the power of ax. cos space bx dy over dx equals ae to the power of ax. cosbx minus be to the power of ax. sinbx space space... left parenthesis straight i right parenthesis dy over dx equals ay minus be to the power of ax. space sinbx fraction numerator straight d squared straight y over denominator dx squared end fraction equals straight a dy over dx minus straight b left parenthesis ae to the power of ax. sinbx plus be to the power of ax. cosbx right parenthesis fraction numerator straight d squared straight y over denominator dx squared end fraction equals straight a dy over dx minus abe to the power of ax. sinbx minus straight b squared straight e to the power of ax. cos space bx fraction numerator straight d squared straight y over denominator dx squared end fraction equals straight a dy over dx minus straight a open parentheses ay minus dy over dx close parentheses minus straight b squared straight y space left square bracket Substituting space be to the power of ax space sinbx space from space left parenthesis straight i right parenthesis right square bracket
    fraction numerator straight d squared straight y over denominator dx squared end fraction space equals straight a dy over dx minus straight a squared straight y plus straight a dy over dx minus straight b squared straight y therefore space space space fraction numerator straight d squared straight y over denominator dx squared end fraction minus 2 straight a dy over dx plus left parenthesis straight a squared plus straight b squared right parenthesis straight y space equals space 0
    Hence Proved




    516 Views
    Answer

    Find the particular solution of the differential equation
    2yex/y dx+ (Y-2xex/y) dy =0
    Given that x=0 when y=1.

    2 ye to the power of straight x over straight y end exponent dx space plus space open parentheses straight y minus 2 xe to the power of straight x over straight y end exponent close parentheses dy space space equals space 0 rightwards double arrow space dx over dy space equals space fraction numerator 2 xe to the power of begin display style straight x over straight y end style end exponent minus straight y over denominator 2 ye to the power of begin display style straight x over straight y end style end exponent end fraction Given space differential space equation space is space straight a space homogenous space differential space equation. therefore comma put space space straight x space equals space vy dx over dy space equals space straight v space plus space straight y dv over dy straight v space plus space straight y dv over dy space space space equals space fraction numerator 2 ve to the power of straight v minus 1 over denominator 2 straight e to the power of straight v end fraction rightwards double arrow space space straight y dv over dy space equals space fraction numerator 2 ve to the power of straight v minus 1 over denominator 2 straight e to the power of straight v end fraction space minus space straight v rightwards double arrow space space straight y dv over dy space equals space minus fraction numerator 1 over denominator 2 straight e to the power of straight v end fraction rightwards double arrow space space 2 straight e to the power of straight v dv space equals negative 1 over straight y dy Integrating space on space both space sides rightwards double arrow space space 2 integral straight e to the power of straight v equals negative integral 1 over straight y dy rightwards double arrow space 2 straight e to the power of straight v space space equals space log space open vertical bar straight y close vertical bar space plus space log space straight C rightwards double arrow space 2 straight e to the power of straight v space equals space log space space open vertical bar straight c over straight y close vertical bar rightwards double arrow space 2 straight e to the power of fraction numerator straight x over denominator straight y space end fraction end exponent equals space log space open vertical bar straight c over straight y close vertical bar Given space that space at space straight x equals 0 comma space straight y equals 1 2 straight e to the power of 0 space space equals space log open vertical bar straight c over 1 close vertical bar rightwards double arrow space straight C space equals space straight e squared therefore comma 2 straight e to the power of straight x over straight y end exponent space equals space log space straight e squared over straight y rightwards double arrow space space log space straight y equals negative 2 straight e to the power of straight x over straight y end exponent plus space 2 rightwards double arrow space straight y space equals space straight e to the power of 2 minus 2 straight e to the power of straight x over straight y end exponent end exponent
    761 Views
    Answer
    Advertisement
    Zigya App

    Find the particular solution of the differential equation
    dy over dx equals negative fraction numerator x plus y space c o s space x over denominator 1 plus s i n space x space end fraction space g i v e n space t h a t space y equals 1 space w h e n space x equals 0

    dy over dx equals negative fraction numerator straight x plus ycosx over denominator 1 plus sin space straight x end fraction rightwards double arrow space dy over dx plus fraction numerator cosx over denominator 1 plus sinx end fraction straight y equals negative fraction numerator straight x over denominator 1 plus sin space straight x end fraction space..... space left parenthesis straight i right parenthesis This space is space straight a space linear space differential space equation space with straight P space equals space fraction numerator cosx over denominator 1 plus sin space straight x end fraction comma space straight Q space space equals negative fraction numerator straight x over denominator 1 plus sin space straight x end fraction therefore comma straight I. straight F. space equals space straight e to the power of integral fraction numerator cosx over denominator 1 plus sin space straight x end fraction dx end exponent equals space space straight e to the power of log space left parenthesis 1 plus sinx right parenthesis end exponent equals 1 space plus space sin space straight x Multiplying space both space sides space of space left parenthesis straight i right parenthesis space by space straight I. straight F. space equals space 1 space plus space sin space straight x comma space we space get left parenthesis 1 plus sinx right parenthesis dy over dx plus straight y space cos space straight x space equals space minus straight x Integrating space space with space respect space to space straight x comma space we space get straight y left parenthesis 1 plus sin right parenthesis space equals integral negative xdx space plus space straight C rightwards double arrow space space straight y space equals space fraction numerator 2 straight C minus straight x squared over denominator 2 left parenthesis 1 plus sinx right parenthesis end fraction space...... space left parenthesis ii right parenthesis Given space that space straight y space equals 1 space when space straight x equals space 0 thus comma 1 space equals fraction numerator 2 straight C over denominator 2 left parenthesis 1 plus 0 right parenthesis end fraction rightwards double arrow space space straight C space equals 1 space space....... space left parenthesis iii right parenthesis Put space left parenthesis iii right parenthesis space space in space space left parenthesis ii right parenthesis comma space space we space get straight y space equals space fraction numerator 2 minus straight x squared over denominator 2 left parenthesis 1 plus sin space straight x space right parenthesis end fraction
    1130 Views
  • zigya switch icon Switch
    • Advertisement
    Advertisement
    Flag Popup Icon
    Flag it
    Submit
    Flag Popup Icon
    Switch to
  • Type
  • Category
    • flexipad
    Share It Icon
    Share it
    Share It
    Share it