Explain the principle of a device that can build up high voltages of the order of a few million volts.
Draw a schematic diagram and explain the working of this device.
Is there any restriction on the upper limit of the high voltages set up in this machine? Explain.
Van de Graaff generator is capable of producing very high potential of the order of 10 MV.
The underlying principle of Van de graaf generator is that a charge given to a hollow conductor is transferred to outer surface and is distributed uniformly over it.
Construction: It consists of a large hollow metallic sphere S mounted on two insulating columns A and B and an endless belt of rubber or silk is made to run on two pulleys P1 and P2 by the means of an electric motor. C1 and C2 are two sharp metallic spikes in the form of combs. The lower comb C1 is connected to the positive terminal of a very high voltage source and the upper comb C2 is connected to the inner surface of metallic sphere S.
Working: When comb C1 is given very high potential, then it produces ions in its vicinity, due to action of sharp points. The positive ions, so produced, get sprayed on the belt due to the repulsion between positive ions and comb C1. These positive ions are carried upward by the moving belt. The pointed end of C2 just touches the belt. The comb C2 collects positive charge from the belt which immediately moves to the outer surface of sphere S. As the belt goes on revolving, it continues to take (+) charge upward, which is collected by comb C2 and transferred to outer surface of sphere S. Thus the outer surface of metallic sphere S gains positive charge continuously and its potential rises to a very high value.
When the potential of a metallic sphere gains very high value, the dielectric strength of surrounding air breaks down and its charge begins to leak, to the surrounding air. The maximum potential is reached when the rate of leakage of charge becomes equal to the rate of charge transferred to the sphere. To prevent leakage of charge from the sphere, the generator is completely enclosed in an earthed connected steel tank which is filled with air under high pressure.
Van de Graff generator is used to accelerate stream of charged particles to very high velocities. But, there is a restriction on the upper limit of high voltage set up in the machine. The high voltages can be built up to the breakdown field of the surrounding medium.
(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence derive the expression for the kinetic energy acquired by the particles.
(b) An –particle and a proton are released from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency? Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees?
a)
The schematic sketch of cyclotron is as shown below:
Electric field: It helps in accelerating the charged particle passing through the gap with the help of an electric oscillator. An electric oscillator imparts the energy to charged particle till it comes out from the exit slit.
Magnetic field: The magnetic force exerts a centripetal force when the accelerated charge particle enters normally to the uniform magnetic field. Centripetal force makes the particle move in a semicircular path of increasing radii in each Dee.
Kinetic energy acquired by the particle is given by,

b)
i) Now, using equation (1), we have
Here we can see that, cyclotron frequency depends upon (q/m) ratio.
So, 
That is, 
ii) Kinetic energy is given by, 
That is, 
That is, proton acquires higher velocity.
(a) Explain, using suitable diagrams, the difference in the behaviour of a
(i) conductor and
(ii) dielectric in the presence of external electric field. Define the terms polarization of a dielectric and write its relation with susceptibility.
(b) A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge Q/2 is placed at its centre C and another charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find
(i) the force on the charge at the centre of shell and at the point A,
(ii) the electric flux through the shell.
When a conductor like a metal is subjected to external electric field, the electrons experience a force in the opposite direction and they accumulate on the left hand side. A positive charge is therefore induced on the right hand side. This creates on opposite electric field ( Ein ) that balances out (E0). The net electric field inside the conductor becomes zero. 
Here, E0 is the external field and Ein is the internal field created by the re-distribution of electrons inside the metal.
Dielctric: When external electric field is applied, dipoles are created for non-polar dielectrics and in case of polar dielectrics dipoles are aligned. An internal electric field is created such that it reduces the external electric field. The placement of dipoles is as shown in the given figure.

The dipole moment per unit volume of the polarized dielectric is known as the Polarization of a dielectric. It is denoted by P.
The formula for polarization is given by, ![]()
b) i) The electric field inside a spherical shell is zero. Therefore, force on the charge placed at the centre of the shell is zero. For a charge placed at A, shell will behave as if the entire charge Q is placed at the centre of the shell.
Therefore, total charge is, ![]()
Distance from 2Q is ‘x’. 
So, according to Gauss’s law,
Total flux, ![]()
A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4 µF and 9 µF capacitors), at a point distant 30 m from it, would equal:
240N/C
360N/C
420N/C
420N/C
C.
420N/C
Resultant circuit,
As, charge on 3μF = 3μF x 8V = 24μC
Charge on 3μF = 3μF x 2V = 18 μC
charge on 4μF +Charge on 9μF
= (24 + 18)μC = 42μC
therefore,
Electric field at a point distant 30 m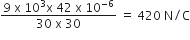
(a) Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Electric dipole moment is the product of either charges or the distance between two equal and opposite charges.
It is a vector quantity.
Electric dipole moment at a point on the equatorial plane:
Consider a point P on broad side on the position of dipole formed of charges + q and - q at separation 2l. The distance of point P from mid-point O of electric dipole is r. 
Let E1 and E2 be the electric field strength due to charges +q and –q of electric dipole.
From the fig. we have
Now, in order to find the resultant electric field, we resolve the components along and perpendicular to AB.
The components perpendicular to AB are sin components and they being equal and opposite to each other cancel each other.
Therefore,
Resultant electric field is given by,
E1 = E1cos θ + E2 cos θ
But, ![]()
From the fig. we can see that,
If dipole is infinitesimal and point P is far away, then l2 can be neglected as compared to r2.
Therefore, ![]()
b) Equipotential surfaces due to an electric dipole is given by,

Electric potential is zero at all points in the plane passing through the dipole equator.
