Book Store

Download books and chapters from book store.
Currently only available for.
CBSE Gujarat Board Haryana Board

Previous Year Papers

Download the PDF Question Papers Free for off line practice and view the Solutions online.
Currently only available for.
Class 10 Class 12

Electrostatic Potential and Capacitance

Three charges of + 0.1 C each are placed at the corners of an equilateral triangle as shown in figure. If energy is supplied at the rate of 1 kW, how many days would be required to move the charge at A to a point D which is the mid-point of the line BC?

Potential at A due to charges at B and C is given by

straight V subscript straight A space equals space fraction numerator 1 over denominator 4 πε subscript 0 end fraction fraction numerator 0.1 over denominator 1 end fraction plus fraction numerator 1 over denominator 4 πε subscript 0 end fraction fraction numerator 0.1 over denominator 1 end fraction space space space space space space space equals space 2 space cross times space 9 space cross times space 10 to the power of 9 space cross times space 1 over 10 volt space equals space 18 space cross times space 10 to the power of 8 space volt

Potential at D due to charges at B and C is given by

straight V subscript straight D space equals space fraction numerator 1 over denominator 4 πε subscript 0 end fraction fraction numerator 0.1 over denominator 0.5 end fraction plus fraction numerator 1 over denominator 4 πε subscript 0 end fraction fraction numerator 0.1 over denominator 0.5 end fraction

space equals space 2 cross times 9 cross times 10 to the power of 9 cross times 1 fifth straight V equals space 36 space cross times space 10 to the power of 8 space straight V

Potential at A due to charges at B and C is given byPotential at D du

Now, V_D–V_A = (36 – 18) x 10⁸V =1.8 x 10⁸V
Work done in moving charge 0.1 C from A to D, W = V.q
W = 0.1 C x 18 x 10⁸ V = 1.8 x 10⁸ J
We know that

Power space equals space Work over Time space space space or space space Time space equals space Work over Power

Time t taken to move the charge from A to D,

space equals space fraction numerator 1.8 space cross times space 10 to the power of 8 straight J over denominator 1 kW end fraction equals fraction numerator 1.8 space cross times space 10 to the power of 8 straight J over denominator 10 cubed space Js to the power of negative 1 end exponent end fraction space equals space 1.8 space cross times space 10 subscript straight S superscript 5 fraction numerator 1.8 space cross times 10 to the power of 5 over denominator 3600 end fraction straight h space equals space 50 space straight h space equals space 50 over 24 space equals space days space equals space 2.08 space days

1312 Views

A dielectric slab of thickness ‘t’ is kept in between the plates, each of area ‘A’, of a parallel plate capacitor separated by a distance ‘d’, Derive an expression for the capacitance of this capacitor for t << d.

Let A is the area of the two plates of the parallel plate capacitor and d is the separation between them. A dielectric slab of thickness t < d and area A is kept between the two plates. The total electric field inside the dielectric slab will be,

straight E space equals space straight E subscript 0 over straight K space equals space straight E subscript 0 minus straight E apostrophe comma

where E’ is the opposite field developed inside the slab due to polarisation of slab. Total potential difference between the plates,

straight V space equals space straight E subscript 0 left parenthesis straight d minus straight t right parenthesis plus Et space space space equals space straight sigma over straight epsilon subscript 0 left parenthesis straight d minus straight t right parenthesis plus straight sigma over kε subscript 0 straight t space space space equals space straight sigma over straight epsilon subscript 0 open square brackets left parenthesis straight d minus straight t right parenthesis space plus space straight t over straight k close square brackets

straight V space equals space straight q over Aε subscript 0 open square brackets left parenthesis straight d minus straight t right parenthesis plus straight t over straight k close square brackets

Let A is the area of the two plates of the parallel plate capacitor a

where q is the charge on each plate.
Since,

straight C space equals space straight q over straight V

or,

straight C space equals space fraction numerator straight q over denominator begin display style straight q over Aε subscript 0 end style open square brackets left parenthesis straight d minus straight t right parenthesis plus begin display style straight t over straight k end style close square brackets end fraction

or,

straight C space equals space fraction numerator Aε subscript 0 over denominator open square brackets left parenthesis straight d minus straight t right parenthesis plus begin display style straight t over straight k end style close square brackets. end fraction

3692 Views

Obtain an expression for the capacitance of a parallel plate (air) capacitor. The given figure shows a network of five capacitors connected to a 100 V supply. Calculate the total charge and energy stored in the network.

An expression for capacitance of parallel plate capacitor.
In the given figure the capacitors C₁ and C₂ in parallel combination
∴ C₁₂ = 1 + 2 = 3
The circuit reduces to

Capacitors C₄ and C₅ are in parallel combinations
C₄₅ = 3 + 3 = 6 μF
Now, the circuit reduces to
An expression for capacitance of parallel plate capacitor. In the gi

Capacitors C₁₂ and C₄₅ are in series combinations.

1 over straight C subscript 1245 space equals space 1 over 6 plus 1 third

Capacitors C₁₂ and C₄₅ are in series combinations.

therefore

straight C subscript 1245 space equals space fraction numerator 3 cross times 6 over denominator 3 plus 6 end fraction space equals space 18 over 9 space equals space 2 space μF

open square brackets because space straight C subscript 5 space equals space fraction numerator straight C subscript 1. space straight C subscript 2 over denominator straight C subscript 1 plus straight C subscript 2 end fraction close square brackets

Now, C₁₂₄₅ and C₃ are in parallel combinations, thus equivalent capacitance is

therefore

straight C space equals space straight C subscript 1245 plus straight C subscript 3 space equals space 2 space plus space 2 space equals space μF

Total energy q = CV

space equals space 4 cross times 10 to the power of negative 6 end exponent cross times 100 space equals space 4 space cross times space 10 to the power of negative 4 end exponent straight C

Energy stored =

1 half CV squared

equals space 1 half cross times 4 cross times 10 to the power of negative 6 end exponent cross times left parenthesis 100 right parenthesis squared equals space 2 space cross times space 10 to the power of negative 6 end exponent space cross times space 10 to the power of 4 space equals space 2 space cross times space 10 to the power of negative 2 end exponent straight J

1256 Views

Two point charges 4Q, Q are separated by 1 m in air. At what point on the line joining the charges is the electric field intensity zero?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q = 2 x 10^–7 C.

Suppose that the point be at a distance x from 4Q charge.
Electric field at P due to charge 4Q = Electric field at P due to Q

box enclose straight E space equals kg over straight r end enclose

Electrostatic potential energy of the system is given as
Suppose that the point be at a distance x from 4Q charge.Electric fie

4089 Views

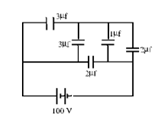
The area of each plate of parallel plate air capacitor is 150 cm². The distance between its plates is 0.8 mm. It is charged to a potential difference of 1200 volt. What will be its energy? What will be the energy when it is filled with a medium of k = 3 and then charged. If it is charged first as an air capacitor and then filled with this dielectric, what will happen to energy?

Given,
Area of each plate of parallel plate capacitor, A= 150 cm²=
Distance between the plates, d= 0.8 mm =

0.8 \times 10^{- 4} m

Potential applied across the capacitor, V= 1200 V

Capacitance, before the dielectric is introduced is given by C_o ,

C_{0} = \frac{ε_{0} A}{d} = \frac{8.85 \times 10^{- 12} \times 150 \times 10^{- 4}}{8 \times 10^{- 4}} = 1.66 \times 10^{- 10} F

Energy stored in the capacitor is,

E_{0} = \frac{1}{2} C_{0} V_{0}^{2} = \frac{1}{2} \times 1.66 \times 10^{- 10} \times (1200)^{2} = 1.2 \times 10^{- 4} J .

When, the capacitor is filled with a medium K and is charged to the same portential V, capacitance is given by,
C = kC₀ = 3 x 1.66 x 10^–10 Farad

Energy stored in the capacitor is given by,

E = \frac{1}{2} {CV}^{2} = \frac{1}{2} ({kC}_{0}) V_{0}^{2} = k \frac{1}{2} C_{o} {V_{o}}^{2} = k (E_{0}) = 3 \times 1.2 \times 10^{- 4} = 3.6 \times 10^{- 4} J

On filling with the dielectric in between, charge remains same and capacitances incresaes thrice of initial value.
Therefore, the potential becomes,

V = \frac{V_{0}}{k} = \frac{1200}{3} = 400 volt

New energy of capacitor, U_fis

U_{f} = \frac{1}{2} {CV}^{2} = \frac{1}{2} ({kC}_{0}) {(\frac{V_{0}}{k})}^{2} = \frac{1}{2} \frac{C_{0} V_{0}^{2}}{k} = \frac{1.2 \times 10^{- 4}}{3} = 4 \times 10^{- 5} J .

284 Views

Chapter Chosen

Book Chosen

Subject Chosen

Book Store

Previous Year Papers

Electrostatic Potential and Capacitance

Two point charges 4Q, Q are separated by 1 m in air. At what point on the line joining the charges is the electric field intensity zero?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q = 2 x 10^–7 C.

Chapter Chosen

Book Chosen

Subject Chosen

Book Store

Previous Year Papers

Electrostatic Potential and Capacitance

Two point charges 4Q, Q are separated by 1 m in air. At what point on the line joining the charges is the electric field intensity zero?Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q = 2 x 10–7 C.

Two point charges 4Q, Q are separated by 1 m in air. At what point on the line joining the charges is the electric field intensity zero?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q = 2 x 10^–7 C.