The box of a pinhole camera, of length L, has a hole of radius a. It is assumed that when the hole is illuminated by a parallel beam of light of wavelength λ the spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size (say bmin) when:
C.
In diffraction, first minima, we have
sin θ = λ/a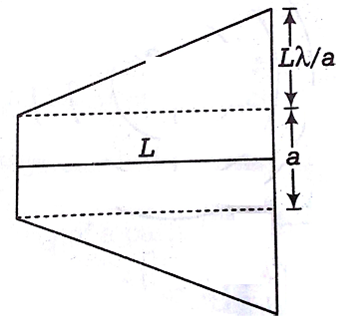
So , size of a spot
b= 2a +2Lλ/a (i)
Then, minimum size of a spot, we get
Radiation of wavelength λ is incident on a photocell. The fastest emitted electron has to speed v. If the wavelength is changed to 3λ/4, the speed of the fastest emitted electron will be:
= v(4/3)1/2
= v(4/3)1/2
A.
According to the law of conservation of energy, i.e. Energy of a photon (hv) = work function (Φ) + Kinetic energy of the photoelectron (mv2/2)
according to Einstein's photoelectric emission of light,
E =(KE)max + Φ
As, hc/λ = (KE)max + Φ
If the wavelength of radiation is changed to 3λ/4
then,
(a) Using Huygens’s construction of secondary wavelets explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a monochromatic beam of light is incident normally.
(b) Show that the angular width of the first diffraction fringe is half that of the central fringe.
(c) Explain why the maxima at 
become weaker and weaker with increasing n.
a) Diffraction of light at a Single slit
A single narrow slit is illuminated by a monochromatic source of light. The diffraction pattern is obtained on the screen placed in front of the slits. There is a central bright region called as central maximum. All the waves reaching this region are in phase hence the intensity is maximum. On both sides of the central maximum, there are alternate dark and bright regions, the intensity becoming weaker away from the center. The intensity at any point P on the screen depends on the path difference between the waves arising from different parts of the wave front at the slit.
According to the figure, the path difference (BP – AP) between the two edges of the slit can be calculated.
Path difference, BP – AP = NQ = 
Angle 
is zero at the central point C on the screen, therefore all path difference is zero and hence all the parts of the slit are in phase.
Due to this, the intensity at C is maximum. If this path difference is, (the wavelength of light used), then P will be the point of minimum intensity.
This is because the whole wave-front can be considered to be divided into two equal halves CA and CB and if the path difference between the secondary waves from A and B is 
, then the path difference between the secondary waves from A and C reaching P will be 
/2, and path difference between the secondary waves from B and C reaching P will again be 
/2. Also, for every point in the upper half AC, there is a corresponding point in the lower half CB for which the path difference between the secondary waves, reaching P is 
/2. Thus, destructive interference takes place at P, and therefore, P is a point of first secondary minimum.
b)
Central bright lies between, 
Therefore, Angular width of central bright fringe = 
So, 1st diffraction fringe lies between 
Therefore,
Angular width of first diffraction fringe is, 
Hence proved.
c) As n increases, part of the slit contributing towards maximum decreases. Therefore, maxima gets weaker with increasing n.
A point object 'O' is kept in a medium of refractive index n1 in front of a convex spherical surface of radius of curvature R which separates the second medium of refractive index n2 from the first one, as shown in the figure.
Draw the ray diagram showing the image formation and deduce the relationship between the object distance and the image distance in terms of n1, n2 and R.
Ray diagram showing the image formation is given below:
The rays are incident from medium of refractive index n1 to another medium of refractive index n2.
NM is taken to be nearly equal to the length of the perpendicular from the point N on the principal axis.
We can have approximation for small angles. We get, 
b)
When the image formed is virtual and n2 > n1
(a) (i) 'Two independent monochromatic sources of light cannot produce a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude 'a' and frequency 'ω', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given by y1 = a cos ωt and y2 = a cos(ωt + ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
(a)
(i) The condition for the sustained interference is that both the sources must be coherent (i.e. they must have the same wavelength and the same frequency, and they must have the same phase or constant phase difference).
Two sources are monochromatic if they have the same frequency and wavelength. Since they are independent, i.e. they have different phases with irregular difference, they are not coherent sources.
ii) 
Let the displacement of the waves from the sources S1 and S2 at point P on the screen at any time t be given by:
y1 = a cos ωt
y2 = a cos (ωt + Φ)
where, Φ is the constant phase difference between the two waves.
By the superposition principle, the resultant displacement at point P is given by:
y = y1 + y2
y = a cos ωt + a cos (ωt + Φ)
=2 a[cos cos 
y = 2 acos 
cos 
... (i)
... (2)
Then, equation (i) becomes:
y = A cos (ωt+
Now, we have:
... (3)
The intensity of light is directly proportional to the square of the amplitude of the wave. The intensity of light at point P on the screen is given by:
I = 4 a2 cos2 (
) ... (4)
(b) Wavelength of monochromatic light = 
Path difference = 
.
So, phase difference,
Intensity of light = K units
Intensity is given by, 
When path difference is 
Intensity of light, I’=
= 
Switch
