Check the continuity of the function f given by f(x) = 2 x + 3 at x = 1.

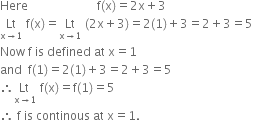
Here    f(x) = x
Function f is defined for all real numbers
Let c be any real number.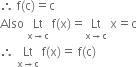

∴ f is continuous at x = c
But c is any real number.
∴  f is continuous at every real number.

Let f(x) = [ x ]. D_f = R
Let a be any real number ∈ D_f.
Two cases arise:
Case I. If a is not an integer, then

⇒ f is continuous at x = a

Case II. If a ∈ 1, then f(a) = [ a ] = a and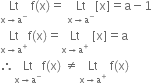

∴ f is not continuous at x = a, a ∈ I.
∴ function is discontinuous at every integral point.

Tips: -

1. Domain of continuity for the function [x] is R – I.
 2. From the graph of [x], done in earlier class, it is also clear that [x] is discontinuous at integral points.