
कोई एक चतुर्भुज, माना ABCD, लीजिए। एक विकर्ण खींचकर, इसे दो त्रिभुओं में बाँटिए। आप छः कोण 1, 2, 3, 4, 5 और 6 प्राप्त करते हैं।
त्रिभुज के कोण-योग वाले गुणधर्म का उपयोग कीजिए और तर्क कीजिए कि कैसे  की मापों का योगफल
की मापों का योगफल  हो जाता है।
हो जाता है।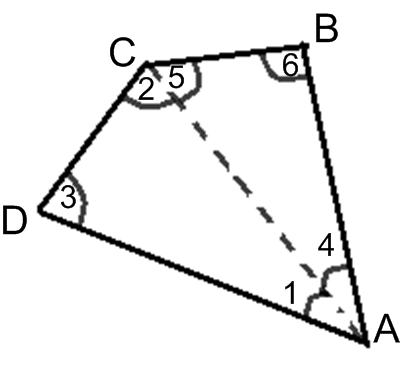

किसी चतुर्भुज ABCD, की गत्ते वाली चार सर्वांगसम प्रतिलिपियाँ लीजिए जिनके कोण दर्शाए गए हैं। इन प्रतिलिपियों को इस प्रकार से व्यवस्थित कीजिए जिससे  एक ही बिंदु पर मिलें जैसा कि आकृति में दर्शाया गया है। आप
एक ही बिंदु पर मिलें जैसा कि आकृति में दर्शाया गया है। आप  के योगफल के बारे में क्या कह सकते हैं?
के योगफल के बारे में क्या कह सकते हैं?
[ टिप्पणी: हम कोणों को  इत्यादि से तथा उनकी मापों को
इत्यादि से तथा उनकी मापों को  इत्यादि से दर्शाते हैं ]
इत्यादि से दर्शाते हैं ]
एक चतुर्भुज के चारों कोणों की मापों का योगफल ______ होता है।
आप इस परिणाम पर अन्य कई तरीकों से भी पहुँच सकते हैं।

चतुर्भुज ABCD पर पुन: विचार कीजिए। माना इसके अभ्यंतर में कोई बिंदु P स्थित है। P को शीर्षों A, B, C तथा D से जोड़िए। आकृति में,  पर विचार कीजिए। हम देखते हैं कि
पर विचार कीजिए। हम देखते हैं कि  ; इसी प्रकार,
; इसी प्रकार,  , से
, से  से
से  और इसका उपयोग करके कुल माप
और इसका उपयोग करके कुल माप  ज्ञात कीजिए। क्या यह आप को परिणाम तक पहुँचाने में सहायता करता है? याद रखिए,
ज्ञात कीजिए। क्या यह आप को परिणाम तक पहुँचाने में सहायता करता है? याद रखिए,  है।
है।

समान सर्वांगसम त्रिभुजों के कटे हुए भाग लीजिए जिनकी भुजाएँ हैं। इन्हें व्यवस्थित कीजिए जैसा कि आकृति में दर्शाया गया है।
आपको एक समलंब प्राप्त होता है। (निरीक्षण कीजिए)
यहाँ पर कौन सी भुजाएँ समांतर हैं? क्या असमांतर भुजाएँ बराबर माप की होनी चाहिए?
इन समान त्रिभुजों के समूह का उपयोग कर आप दो और समलंब प्राप्त कर सकते हैं। उनको ढूंढ़िए और उनकी आकृतियों कि चर्चा कीजिए।


दो समान समांतर चतुर्भुजों के कटे हुए भाग A'B'C'D' तथा लीजिए

यहाँ पर भुजा  , भुजा
, भुजा  के समान है परंतु इनके नाम अलग-अलग हैं। इसी प्रकार, दूसरी संगत भुजाएँ भी समान हैं।
के समान है परंतु इनके नाम अलग-अलग हैं। इसी प्रकार, दूसरी संगत भुजाएँ भी समान हैं। को
को  के ऊपर रखिए। क्या वे एक दूसरे को पूर्णतया ढकती हैं? अब आप
के ऊपर रखिए। क्या वे एक दूसरे को पूर्णतया ढकती हैं? अब आप  तथा
तथा  की लंबाई के बारे में क्या कह सकते हैं?
की लंबाई के बारे में क्या कह सकते हैं?
इसी प्रकार  तथा
तथा  की लंबाई की जाँच कीजिए। आप क्या पाते हैं?
की लंबाई की जाँच कीजिए। आप क्या पाते हैं?
समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर माप की होती हैं।
