If the mth term of an A. P. is  and nth term is
and nth term is  then show that its (mn)th term is 1.
then show that its (mn)th term is 1.
Let x and d be the first term and common difference respectively of the AP, respectively.
Then,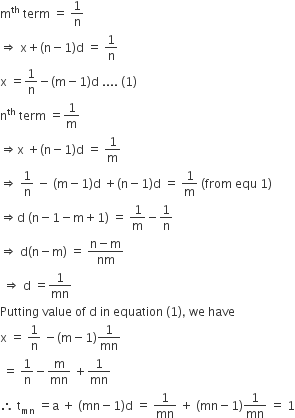
The ratio of the sums of the first m and first n terms of an A. P. is m2: n2. Show that the ratio of its mth and nth terms is (2m−1):(2n−1).
Let Sm and Sn be the sum of the first m and first n terms of the A.P. respectively. Let, a be the first terms and d be a common difference.
⇒[2a+(m−1)d]
n =[2a(n−1)d]m
⇒2an+mnd−nd=2am+mnd−md
⇒md−nd=2am−2an
⇒(m−n)d=2a(m−n)
⇒d=2a
Now, the ratio of its mth and nth terms is
Thus, the ratio of its mth and nth terms is 2m – 1 : 2n – 1.
Find the 60th term of the AP 8, 10,12, ..., if it has a total of 60 terms and hence find the sum of its last 10 terms.
The given AP is 8, 10, 12, ....
So,
First term =a = 8
Common difference = d = 10-8 =2
We know that nth term of an AP, an = a + (n - 1)
60th term of the given AP = a60 = 8 +( 60-1) x 2 = 8 + 59 x 2 = 8 + 118 = 126
Therefore, the 60th term of the given AP is 126
It is given that the AP has a total of 60 terms. So, in order to find sum of last n terms. we take
First term, A = 126
Common difference, D = -2
Now,
The sum of four consecutive numbers in an AP is 32 and the ratio of the product of the first and the last term to the product of two middle terms is 7 : 15. Find the numbers.
Let the numbers be (a -3d),(a-d), (a+d) and (a+3d)
∴ (a-3d) + (a-d) +(a+ d) + (a +3d) = 32
⇒ 4a = 32
a = 8
If d =2 numbers are : 2, 6,10, 14
If d = -2 numers are 14,10,16,2
